Wednesday, May 28, 2008
Tips for the "new" 7th grade AEP!
Then provide a name, either you or one of your peers to organize the data (tips) and reorganize it in a manner that will be meaningful for our new group.
thx,
Ms. Leckman
Friday, May 02, 2008
Re-visit Function This Function That
 Ms. Leckman
Ms. Leckman8th Grade POW
IMPORTANT!!! Be careful, some of the 7th grade questions ask for names - I WILL NOT POST WITH TEACHERS NAMES OR INTIALS. However you may discuss tough content areas and how to make themselves and their teachers happy to ensure a success and or pleasant 8th grade year. :-)
Here is your second task:
Think of a function as a math machine with an input and an output. Suppose the function is A(x) = 3x + 1. That means if you put any number (x) into this function machine, the machine will multiply the number by three and add one. For example, what is the output if five is the input? Five times three plus one equals 16 for the output. That's written A(5) = 16.
Suppose you join two function machines so that the output of the first one is connected to the input of the second one. Let's make the second function B(x) = x^2, (remember that x^2 means x squared). If you put two into the A machine, out comes seven. Then seven is the input to the B machine which squares it, and out comes 49. Okay? That's written B(A(2)) = 49.
Here are five functions:
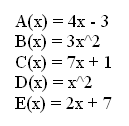
I am going to connect them in alphabetical order and use two as the input number. That would be written as E(D(C(B(A(2))))). The resulting output = 553,359.
What arrangement of functions will produce the largest output? Let x = 2 (or your input.) Each function used only once. I am looking for logical reasoning and algebra rather than just guess and check. Explain why you chose your particular arrangement. (Make sure to include your function in well formed, symbolic notation.)
7th Grade POW
Ms. Leckman decided that the Math Club mascots, Fibonacci and Descartes, had outgrown their 10-gallon home, so this weekend she picked up a 15-gallon aquarium at a flea market. Oliver and Suzanne have been assigned the task of setting up the new aquarium. They have been instructed to fill it exactly three-quarters of the way to the top. Fibonacci and Descartes will be transferred with some of the water from their current environment to help them adjust to their new home. Unfortunately, Suzanne and Oliver can not find a clean bucket for carrying water to the aquarium. All they can find are two eight-ounce glasses. Working from the sink to the left of the aquarium stand, Suzanne takes 45 seconds to fill one glass and dump it into the aquarium. Working from the sink to the right of the aquarium, Oliver can fill one glass and dump it into the tank in 39 seconds.
If Suzanne and Oliver start at noon and keep working at these constant rates, what time will they complete their task? Which student will add the last glass of water?
Friday, April 25, 2008
Asking 8th Graders
Question one needs to be regarding success in the 8th grade.
Question two needs to be regarding 8th grade Honors Math class.
And the final question is anything you want.
Make sure that no one has asked any of your questions. Each question needs to be unique.
Ms. Leckman
Friday, April 11, 2008
Welcome back!!!!!!!!!!
Today you will be completing two tasks. The first task is to present your perspective on AIMS assessments. The second is a math problem. Be sure to fully explain your answer, that means show how you got your answer. If you use symbolic notation understand that an equation is a tool to support proof. Explain what each of the parts of your equation represent and why they are important or why you have considered these factors.
PART 1
Here are questions I would like you to address:
1. Do you like AIMS?
2. Does AIMS show what you personally know?
3. If you wanted to demonstrate what you have learned this year - how would you go about
proving your new mathematical understandings?
PART 2 - THE PROBLEM
Saturday, March 29, 2008
Bye Bye Blog
Friday, March 14, 2008
Math without Mathematicians?
Although we engage in learning mathematics every day, we never stop to think about the fact someone actually took the time to figure out the structures, connections, and rules of mathematics so that we could use it without having to re-figure it out every time. Here is your task for the day. Follow these links for historical information:
http://www.agnesscott.edu/Lriddle/women/women.htm
http://www-groups.dcs.st-and.ac.uk/~history/index.html
http://www-groups.dcs.st-and.ac.uk/~history/BiogIndex.html
http://math.about.com/od/mathematicians/Mathematicians.htm
Explore some of the mathematicians or the mathematicians related to a genre of mathematics. Give us a peak into the world of three mathematicians. Be sure you understand what it is they really contributed to mathematics before you post. (This is why you may want to search by topic.)
In your write up please include the following:
Name
Era
Branch of mathematics
A interesting fact about the mathematician
How their contribution helps us today, give a real life example of the mathematics, or explain How their contribution has shown up in our studies.
You may not cut and paste. These are written in your own words in paragraph form, including correct spelling and puncuation. I can't wait to read what you find out about the eclectic world of mathematicians.
Ms. Leckman
P.S. Don't forget to make a major and minor edit to the wiki.
ENJOY YOUR BREAK!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
SEE YA IN 9 DAYS. :-)
Friday, March 07, 2008
How Did They Know?????

Friday, February 29, 2008
And now for something completely different
http://muchadoaboutmath.wetpaint.com/
Today we will also be looking at what you know and what you do not know. Today will provide a way for you to know what to practice prior to our Benchmarks and AIMS. Please follow the links to the practice tests. These test will provide feedback for you immediately so you have an idea where your strengths and refinement areas lie.
When you find your refinement area you can use your books or the online activities and 'How to's' to improve your understandings.
McDougal Littell
http://www.classzone.com/books/algebra_1/index.cfm
MAC 8th Grade
http://www.glencoe.com/sec/math/msmath/mac04/course3/index.php/az/2004
MAC 7th Grade
http://www.glencoe.com/sec/math/msmath/mac04/course2/index.php/az/2004
Please print the scores to your section assessments and bring them to me. Make sure your names on them.
Please let me know if you need any assistance.
Ms. L.
Friday, February 15, 2008
Pool Tables
Marisa created a game called Paper Pool. Her pool tables were rectangles drawn on grid paper. The pockets at each corner were labeled A (lower left), B (lower right), C (upper right), and D (upper left). Marisa described each table by its size, giving the horizontal length first and the vertical height second. The figure below shows a 6 × 4 table.

How to Play Paper Pool
• The lower-left corner is always corner A, and the labeling continues counterclockwise
with B, C, and D.
• The ball always starts in corner A.
• The ball is hit with an imaginary cue (a stick for hitting a pool ball) so that it travels at a
45° diagonal across the grid.
• If the ball hits a side of the table, it bounces off at a 45° angle and continues its travel.
• The ball continues to travel until it hits a pocket.
Link to webpage:
http://illuminations.nctm.org/ActivityDetail.aspx?ID=28
Link to handouts:
http://juliesgotmail.googlepages.com/home
Questions:
1. In what corner will the ball stop?
2. How many hits will have occurred by the time the ball stops?
3. Write rules (equations) that you could use to determine what will happen to the ball as it travels on a table of any size. Your rules (equations) should tell you, without drawing the path, the corner at which the ball will stop and the number of hits that occurred. (These might be separate equations.)
Support your answers with examples in the form of patterns, spreadsheets, tables, graphs and or illustrations.
If you have any questions please see me.
Ms. Leckman
Here is a short video with some of your responses. My video will go fast so be prepared to use the pause button to spend a minute or two on a solution. I will be posting these on our class webpages to see if we can get a larger view. :-)
K.A. Video
Enjoy. I will try to post more video this year. :-) Yes, I truly am a nerd, I try to learn new "stuff" (sorry Mrs. Campbell) all the time. :-)
Ms. L.
Friday, February 01, 2008
Star Light Star Bright
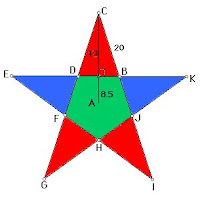
Martha Stewart wants to rebuild her ugly garden. She thinks it needs a modern twist and decides to make a star-shaped garden where the legs of the star will be filled with flowers and the central pentagon will be grass.
Martha needs your help to calculate the floral area and grassy area in this new garden design. Then she can figure out the equipment and materials she will need for the project.
To form this star, simply extend the sides of the pentagon to make the legs of the star. Here are the dimensions of her stellar garden:
each leg of the star is a triangle with two sides, both 20 feet long, and an height of 19 feet.
The pentagon is regular (the sides are all equal and the angles are all equal),
and the distance from the center of the pentagon to one of the sides is 8.5 feet.
To the nearest square foot, what are the areas of Martha's flower section and grass section. Because Martha is not sure what she would like to do, please provide three different ways she could arrange her garden, be sure to let her know the area each floral and grass area will take. Explain how you solved one of the area problems. BE SPECIFIC! Walk us through all of your steps.
HERE ARE SOME OF YOUR SOLUTIONS:
What are the odds????

Friday, December 07, 2007
POW Dec 3

Nice job guys! Many of you not only found the correct answer but were moving towards the correct algrithm. Here is the answer for this weeks blog. have a great weekend!
Ms. L.
Correct answer:7 kids * 2 legs = 14 legs
7 kids * 7 rucksacks = 49 rucksacks
49 rucksacks * 7 big cats * 4 legs = 1,372
legs49 rucksacks * 7 big cats * 7 small cats * 4 legs = 9,604
legs14 + 1,372 + 9,604 = 10,990 legs total.
This may also be shown as a simple powers of 7 problem:
Total legs = 7^1 * 2 + 7^2 * 0 + 7^3 * 4 + 7^4 * 4. This is because there are:7^1 * 2 kids legs7^2 rucksacks (But they don't have legs)7^3 * 4 big cat legs7^4 * 4 small cat legsOf course, 7^2 * 0 could be omitted completely, but I include it just to show the progression of powers of 7.
Friday, November 30, 2007
7th Grade Nov. 26th
A banana farmer has six monkeys who hate each other. They must be kept in pens to separate them from the bananas as well as from each other.
The farmer has created six pens of equal size using 13 equal lengths of fencing. The pens are organized in a row.


How can the farmer reorganize the fencing to make six new pens of equal size with the 12 remaining lengths of fencing?
Have fun. Remember to back up your document in the TO BE GRADED file and submit your responses to:
Ms. Leckman
Thursday, November 15, 2007
7th and 8th Grade POW Nov. 12th
I have a number of post from the 7th Grade class that have no names. :-( If one of the POWs is yours and there is no name on it you MUST see me. Mid terms are coming out if you want credit for this POW, see me before the break!!!
P.S. See below for further submission check out the final submission!
Good Luck with the problem.
Ms. L.
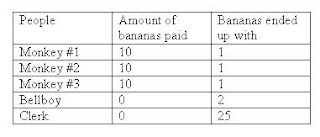
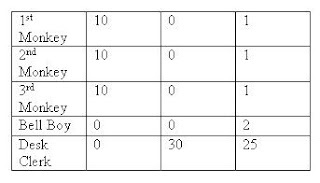
Three monkeys walk into a motel on the Planet of the Apes and ask for a room. The desk clerk says a room costs 30 bananas, so each monkey pays 10 bananas towards the cost.
Later, the clerk realizes he made a mistake, that the room should have been 25 bananas. He calls the bellboy over and asks him to refund the other 5 bananas to the 3 monkeys. The bellboy, not wanting to make a mess dividing the 5 bananas three ways, decides to lie about the price, refunding each monkey 1 banana, keeping the other 2 bananas for himself. Ultimately each monkey paid 9 bananas towards the room and the bellboy got 2 bananas, for a total of 29 bananas. But the original charge was 30 bananas.
Where did the extra 1 banana go?
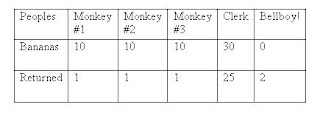
When the monkeys entered they paid the fee of 30 bananas, but the clerk made a mistake and it was 25 bananas so he gave the 5 bananas to the bellboy to give back evenly. But he didn’t, to make it easier on himself he decided to give 1 to each monkey and keep the two to himself.
So when I plotted on the table missing bananas, you find out if you add it up you find there was no missing banana! ~!!YAY!!~
The equation is 29=9x3+2
By AH

Friday, November 09, 2007
8th Grade POW Nov. 5th
The problem this week is an old one, in fact over 500 years old. It goes back to the days in Europe when fairs were common in many cities, and merchants would travel from city to city, selling their various goods and buying other items they desired.
It seems that a humble merchant visited three fairs. At the first fair, early in the morning, he doubled his money selling his products, but spent $30 in food and buying other items.
At midday at the second fair, he tripled his money and spent $54. At the third fair in the afternoon he quadrupled his money but spent $72.
Upon his return home to his wife and ten children, late that day, he counted the money he had in his bag; there was $48.
 Now, if the merchant returned home with a profit his wife was happy and she was sad if he returned home with less money than when he started with. So tell me: was his wife happy or sad when he returned? And how much did the man gain or lose, respectively?
Now, if the merchant returned home with a profit his wife was happy and she was sad if he returned home with less money than when he started with. So tell me: was his wife happy or sad when he returned? And how much did the man gain or lose, respectively?Remember: although this type of problem could be solved by guess-&-check or reverse analysis, such an approach will not be accepted here. (You may use them separately to verify your answer; however substitution would be the best way to check your answer.) You must construct an equation for credit. Make sure to label the steps for your solution.
Extra Credit (this is very easy this week don’t over look the opportunity!): If you did your work straightforwardly, your next-to-last step of equation work was of the form (m) x = n. The number “n” is in some way rather interesting; what is it?
Extra Credit: The next-to-last step is where Ax=B (24m=696) is interesting because B (696) is a palindrome. If you do not know what a palindrome is please look it up, it is not just a Language Arts phenomenon. :-)
Monday, November 05, 2007
7th Grade POW for November 5th
 Ann and Sue bought identical boxes of stationery. Ann used hers to write one sheet letters, and Sue used hers to write three sheet letters. Ann used all the envelopes and had 50 sheets of paper left, while Sue used all of the sheets of paper and had 50 envelopes left. How many sheets of paper and how many envelopes were in the box to begin with?
Ann and Sue bought identical boxes of stationery. Ann used hers to write one sheet letters, and Sue used hers to write three sheet letters. Ann used all the envelopes and had 50 sheets of paper left, while Sue used all of the sheets of paper and had 50 envelopes left. How many sheets of paper and how many envelopes were in the box to begin with?Make sure to thoroughly explain how you solved the problem. Show your mathematics and explain as you go so we understand what the numbers are and where you got them or why they are important.
Good luck,
Ms. L.
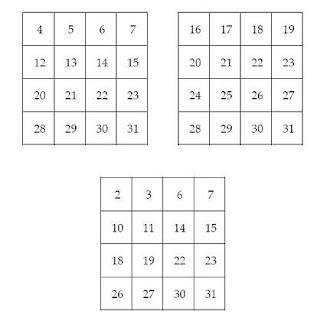
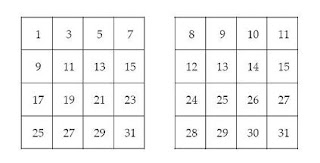
To begin the problem you had to account for the proportions or ratios of items to solve the problem. Anne used one piece of paper per letter and Sue used three pieces of paper per letter. If you thought about the number of materials per letter you could set up a table of paper and envelopes per letter. Doing so you would want to add 50 to the number of papers Anne used because she had fifty left over, and you would want to add 50 to Sue’s envelopes as she had 50 envelopes left over. Then all you needed to do was test various numbers of letters, and continue until the total paper and total envelopes were the same for both girls.
Here is the table I made. You can see from the table the girls started with 150 pieces of paper and 100 envelopes.
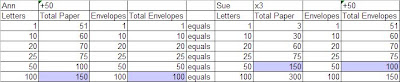
Here is another table done by AH:
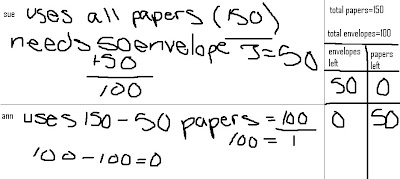
Trying to find the best way
I have begun reading your posts for last week. I am trying to determine the best way to post these. I may begin a website just for the postings that tend to be multi-media. Give me a couple days to figure this out, I will keep you posted in class.
ms.l.
Saturday, October 27, 2007
Rubric for the To Kill a Mockingbird Blog response
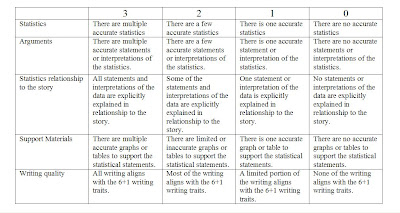
What's my line?