IMPORTANT!!! Be careful, some of the 7th grade questions ask for names - I WILL NOT POST WITH TEACHERS NAMES OR INTIALS. However you may discuss tough content areas and how to make themselves and their teachers happy to ensure a success and or pleasant 8th grade year. :-)
Here is your second task:
Function This Function That
Think of a function as a math machine with an input and an output. Suppose the function is A(x) = 3x + 1. That means if you put any number (x) into this function machine, the machine will multiply the number by three and add one. For example, what is the output if five is the input? Five times three plus one equals 16 for the output. That's written A(5) = 16.
Suppose you join two function machines so that the output of the first one is connected to the input of the second one. Let's make the second function B(x) = x^2, (remember that x^2 means x squared). If you put two into the A machine, out comes seven. Then seven is the input to the B machine which squares it, and out comes 49. Okay? That's written B(A(2)) = 49.
Here are five functions:
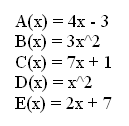
I am going to connect them in alphabetical order and use two as the input number. That would be written as E(D(C(B(A(2))))). The resulting output = 553,359.
What arrangement of functions will produce the largest output? Let x = 2 (or your input.) Each function used only once. I am looking for logical reasoning and algebra rather than just guess and check. Explain why you chose your particular arrangement. (Make sure to include your function in well formed, symbolic notation.)
16 comments:
RS
Ok so the arrangement that I chose was:
2x+7
7x+1
4x-3
3x^2
x^2
or E(C(A(B(D(2)))))
The approach that I took to this problem was that I would wait and use the functions with exponents at the end because there would be bigger #'s to square at the end. It would be more effective to get bigger #'s. So right then i knew that functions B and D would be at the end. Then I looked at the coeficients of the functions that were left. Because function E had the lowest # coeficient, I decided to put that first. Then, to get the # raised higher for the exponents, I used function C. With only one function left, funcion A, I put that one right in the middle. I came out with an answer of 82,049,592,249. This was the first one I tried. I was pretty sure this order was right, but I went ahead and tried a few more combinations. I didn't find one higher than this.
A.H. and K.B.
The simple answer for this 5 – function equation, resulting in the highest possible value, is B(D(C(A(E(2))))). We arrived at this equation due to a simple process.
First, we wrote out all of the functions. Then we plugged in 2 for each of the values to get an overall view of the equation. We decided that we would use the equations with exponents first, starting with 3x^2 then x^2. Then we plugged in numbers in the remaining equations to analyze how they changed over time. We realized that we would want the highest value for the next equation. That’s how we got our final solution. By the way, the answer is - 20,639,121,408
Posted by –
A.H. and K.B.
:):):):):):):):):):):):):):):):):)
K.A.
E=11
11 into C=76
76 into A=301
301 into D=90601
90601 into B=24625623603
d.c.
first i wrote out and sloved all of the functions using 2 for (x). then i order the functions biggest to smallest. the small function i put on the inside and i put the biggest one on the out side. the thing that i came up with was B(D(C(A(E(2))))). and then you would work you way out. A=5, B=12, C=15, D=4, E=11. and when you plug it all in it would be
12(4(15(5(11(2))))). and the answer to that is 20,639,121,408.
E(x)=2x+7
A(x)=4x-3
C(x)=7x+1
D(x)=x^2
B(x)=3x^2
61917364224
B(D(C(A(E(2))))) = 61917364224
I FOUND THIS OUT BECAUSE I TOOK THE EQUATION THAT WOULD PRODUCE THE SMALLEST TOTAL THEN I WENT ALL THE WAY TO THE HIGHEST. BECAUSE IF YOU WOULD TAKE THE NUMBER AND SQUARE IT THE YOU WOULD GETA SUPER HUGE NUMBER THEN IF YOU WOULD TIMES IT BY 3 AND THEN SQUARE IT AND YOU WOULD GET AN OMEGA SUPER HUGE NUMBER. AND THAT IS HO I FOUND THE BEST EQUATION TO GET THE HIGHEST TOTAL
IW
A(x) = 4x-3
B(x) = 3x2
C(x) = 7x+1
D(x) = x2
E(x) = 2x+7
Largest answer is ECADB
2(2)=
4+7=
11(7)=
77+1=
78(4)=
242-3=
2392=
571212=
326,808,641(3)=
9,788,425,923
d.c.
First I wrote out and solved all of the functions using 2 for (x). Then I order the functions biggest to smallest. The small function I put on the inside and I put the biggest one on the out side. You are putting the biggest expontional on the outside and the smallest one on the inside. The thing that I came up with was B(D(C(A(E(2))))). And then you would work you way out. A=5, B=12, C=15, D=4, E=11. And when you plug it all in it would be 12(4(15(5(11(2))))). And the answer to that is 20,639,121,408.
L.N & J.S
My order: E (C (A (B (D (2)))))
At first, we decided to do the exponents last because we knew that the number would be larger. Our final equation wasn’t the one that we thought would create the larger number. We actually had the B and D switched around.
The answer for equation E came out as 11. Then we put that into equation C, which equaled 78. Then we got 309 by inserting the 78 into equation A. Then with equation D we got 95,481. Then that squared came out as: 82,049,592,249. That was the largest answer that can be made. ((:
J.B.
A(x) = 4x-3
B(x) = 3x2
C(x) = 7x+1
D(x) = x2
E(x) = 2x+7
2(2)=
4+7=
11(7)=
77+1=
78(4)=
242-3=
2392 =
571212 =
326,808,641(3)=
9,788,425,923
E.H.
The order in which you would place the functions is b, c, a, e, d I did not reach this conclusion by guess and check but by a different method. I knew that b would give me the largest value if I plugged in two, because when I solved it, it came to 64 , then I knew it was c next because if you solve it, it comes to 15 , then a because when that is solved it comes to 5 , and it is the next greatest value when 2 is plugged in, I then plugged 2 in to each until I found the pattern of greatest answer to lowest, which gave me my answer.
D.M. and E.Mu.
Todays POW wanted us to find the best equation that will give us the highest number. We decided to start by finding what 2 would give us in each equation, A-E. We got the values, then decided to order them. We started with the equation that had the lowest coefficient, E. We then picked equation C because it would bring low number up. The next equation we picked was the middle coefficient with no exponent because it still had no exponent, A. Then we used the exponent equation with the highest coefficient so we would get a high number, B. We had only one equation left, D, then we plugged it in. It was left to the end so we had the highest number possible squared at the end. Our equation looked like, D(B(A(C(E(2))))). Our final number was 82,049,529,249.
This was our POW for this week.
M.G.
A.R.
This weeks P.O.W. wanted us to figure out what alphabetical order will give us the greatest output. The equation they gave us to start with was E(D(C(B(A(2))))). They also gave us five functions to work with. First, what we did was plug in 2 to all five of the functions because the P.O.W. said x=2. Are answers were A=5, B=12, C=15, D=4 and E=11. Next what we did was start to figure out the order we wanted to use we decided that the equations with the exponents would be first. We wanted the order to start with the leading coeffecient so our order is B(D(C(A(E(2))))). We then decided to solve the equation by plugging in the numbers into the equation so u put 12 into the equation D which then equals 144 then u put that into C which is 1009 then you put that into A which is 4033 then you put that into equation E which is 8067.
A.L.
Today’s POW was about combining parts of equations to find an answer higher than 553,359. I started with solving for A,B,C,D, and E. After that, I tried putting the five in different orders. I tried multiple times, and failed each time. Finally, I just decided to start making random orders, and found one that had a higher output than all the rest. That order was E(C(A(B(D(2))). It equaled 82,049,592,249
A(x)=4x-3
A(2)=4(2)-3
A=5
B(x)=3x^2
B(2)=3(2)^2
B=12
C(x)=7x+1
C(2)=7(2)+1
C=15
D(x)=x^2
D(2)=2^2
D=4
E(x)=2x+7
E(2)=2(2)+7
E=11
E(D(C(B(A(2))))
=553,359
B(D(C(A(E(2))))
B(D(C(A(11)))
B(D(C41))))
B(D(288))))
B(82944)
20,639,131,408
E(C(A(B(D(2))))
E*2
C*11
A*78
B*309
D*286443
82,049,592,249
DGT and AM
(C)(A)(B)(E)(D) We found this by finding the equation that was the largest, and then finding all the equations after it and lining them up from largest to smallest. This would result in the largest number possible.
JJ
What i did was i took the smallest answer and then multiply the next biggest and so on. Like this
E
A
C
D
B
and i got 61917364224 for the answer
CT&DG
The order was:
B(D(C(A(E(2))))
We choose this order because we wanted to use the exponents first so the number would be larger. That way the number would become larger and then the coefficiants would make the number grow even more
Post a Comment