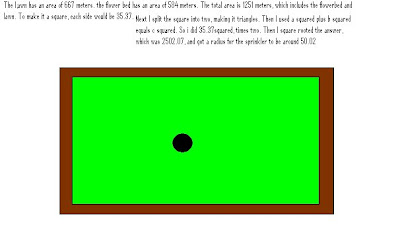
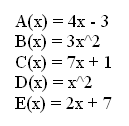The first is the most important and is required. You will determine how much it would cost to purchase all the items in the song, The Twelve Days of Christmas. Go to the following site to find the unit cost of each of the items in the song. Then determine how much it would cost in total, for all the items. Here is a site that will tell you this years costs for these items:
http://www.pncchristmaspriceindex.com/CPI/index.html
A couple of tips:

You may want to use excel to help in this task.
If you use excel save it and send it to our mathclasshonors@yahoo.com mailbox (include your name!!!) and I will give you extra credit!
BIG, BIG, BIG!!!! Remember that you that you will be purchasing a partidge in a pear tree on the first day, but on the second day of christmas you buy two turtle but you buy another partidge in a pear tree.
Task Two - Extra Credit:
Develope your own Twelve Days of Christmas. Create a list of what you would buy your "True Love" on the Twelve Days of Christmas and find out what it would cost you for these items. REMEMBER: If you buy, one the first day of Christmas the Batman the Dark Night, then for the second day you buy, Guitar Hero you have to buy them another Batman the Dark Night.
Task Three: This one is also extra credit.
Here is a list of online snowflake makers. (They are very fun, I tried each one myself!) You may play on the sites. Make some snowflakes. When you have made one you really like download or copy it, and then print it.
http://snowflakes.barkleyus.com/
http://www.zefrank.com/snowflake/
http://www.popularfront.com/snowdays/
http://gwydir.demon.co.uk/jo/symmetry/snow.htm
http://compute2.shodor.org/cgi-bin/snowflake/snowflake.pl
Now make a list of all the geometric properties and attributes contained in the snowflake. You may want to do a bit of research on snowflakes to find some of these properties. This is the important part and this is where I will determine the value of the extra credit. The snowflake itself is worth no extra credit points!
Have fun!
Ms. Leckman
P.S. The extra credit is due Monday!