Reflection September 28th

Feeling like you are working too hard? Your probably not alone. Today we will not be doing a Problem of the Week, instead we will try to help each other. Here are your tasks for today. Do not copy and paste this writing into your reply!!!!

1. Look through your book and identify a couple areas you need help in for the assessment next week. (For 8th Grade: remember that the assessments are cumulative so that means there may be problems you would want help with from chapter one as well as chapter two.) You will need to post three questions or requests for help. (I can't think of one of you that should not be able to find three things you need help with... so don't go there. :-) ) You will want to find a problem in the book that illustrates the type of help you need.

2. You will go to the "I get by with a little help from my friends" blog and post your responses under the correct book and chapter/investigations. Post an example problem in your reply and explain what you need help understanding.

3. Make sure you post your reply under the correct chapter and book.

4. Next, find and respond to at least three post that need help. Be complete and give them as much help as you can.

5. Make sure to put your intials at the top of each of your posts so I can easily find them. (Thank you in advance.)

Good luck! Ms. L.

More about last weeks post

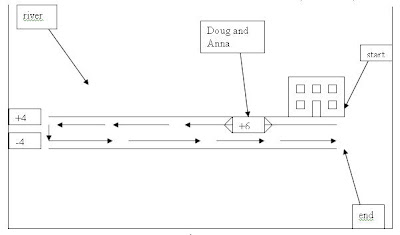
Most of you realized there was a pattern involved with the Frog Puzzle, yet many of the explanations did not really address providing any direction or ways to solve the problem. Determining what a string of numbers as an explanation to the problem (ie... 1,2,3,4,5) were trying to say really didn't help us identify or understand which frog was moving and where the frogs were moving to. I will be adding peoples visuals to see if this helps us understand what was happening in the problem and how we might better explain and describe the actions and pattern. A good way to see if your explanation is sufficient, give you parents or a friend your written explanation and take them to the web site. Ask them what helped them understand how to win and might have been incomplete or insufficient directions. (Extra Credit: Write up the discussion you have with your parents and have them sign it for extra credit this week. Yes, don't even ask, complete sentences and correct punctuation and spelling are required.)

Last weeks POW was actually a version of a very old puzzle - The Tower of Hanoi or Towers of Hanoi. The Towers of Hanoi are a mathematical game or puzzle. It consists of three pegs, and a number of disks of different sizes which can slide onto any peg. The puzzle starts with the disks neatly stacked in order of size on one peg, the smallest at the top. The objective of the game is to move the entire stack to another peg. Easy, maybe but you have to follow the following rules: You may only move one disk at a time. You may only move the top disk from one of the pegs and sliding it onto another peg, it can be placed on another disk that may already be present on that peg. And finally, no disk may be placed on top of a smaller disk.

The puzzle was invented by the French mathematician Edouard Lucas in 1883. There is a legend that accompanies the game. It states there is a temple which contains a large room with three posts that contain 64 golden disks. According to the legend, when the last move of the puzzle is completed, the world will end. The priests of Brahma, acting out the ancient prophecy and have been moving these disks, in accordance with the rules of the puzzle. There are patterns which repeat the action over and over again, we call these iterative patterns. The Towers of Hanoi are a type of iterative pattern called a recursive pattern. A recursive pattern is a pattern that repeats itself but you have to have the results of the previous action or term to determine the outcome of the output or term you are solving for. This type of patterning is very common in computer programming and The Tower of Hanoi is a problem often used to teach beginning programming.

If you would like to try the original puzzle click on the link below:
http://www.vtaide.com/png/lesol/games/tower/hanoi-2j.html

Ms. Leckman

POW for the Week of September 17th

Let's do something a bit different this week. The POW this is week is to explain how you solved the game found at the link below. To receive credit for this weeks POW you must explain how to get all 12 frogs across all the lily pads. Include any diagrams, tables, or illustrations that help explain what you did. Have fun and come to class ready to post your answer! :-)

Ms. Leckman

Games away:
http://www.hellam.net/maths2000/frogs.html

Sept 4th POW

Ready, good. :-) Here is this weeks POW. Remember:
You may think about the problem.
You may try to solve the problem.
You may not post your responses until Friday while we are in the lab.

Mathematics Club Membership

Before the start of the fall membership drive, Mrs. Roberts wants to know how many students are in the Mathematics Club.

She asks the president of the club, "What's your membership?"

The president replies, "twice our number plus half our number plus a quarter of our number plus you is one hundred."

"Great," says the Principal, "that is exactly one more than one eighth of our total student enrollment here at Madison Number One Middle School."

Please address all of the following in your response:

1. How many students are enrolled at Madison Number One Middle School?
2. How many students are in the Math Club?
3. Write an equation that will help you either find or justify your answer.

Be sure to use comprehensive explainations when you explain how you found each answer. Good Luck. Ms. L.

POW August 31st

You all did a nice job on last weeks problem. Here is a problem that you can use some of the "tools" we have been talking about in class. They may come in handy in solving this problem.
:-) Good luck.
Ms. L.

P.S. Ma ke sure to put both you and your partnership intials in the box you submit your answers. I can't give you credit if I don't know who posted the response. :-)

Here is the POW for this week:

Doug and Anna plan to kayak on the river near their home. The river flows at a rate of 4 miles per hour. In still water they paddle their kayaks at a constant rate of 6 miles per hour. They start and end their trip at the same place on the river. They kayak for exactly two hours, first going upstream and then downstream. What is the total length, in miles, of their trip on the river? Express your answer as a decimal to the nearest hundredth.


You guys did a very nice job this week. Many of you were able to see that the distance there and back needed to be equivalent. The idea of writting them as two equations was a new idea to some of you. Here are two ways to look at the solution to this weeks problem.

Here are some of your peers graphs and tables. :-)

POW Aug. 20th

O.k. so here is your first POW. I know all of you have received an e-mail like this one, but why do they work? Your task is to mathematically explain this quandary. Be as specific and concise as you can. (Remember - save a copy of your work in Word just in case. :-) and use your first and last initial ONLY!!!!)

Ms. JL


Many of you sent in excellent solutions to this problem!!! You tackled it using logic, order of operation, and algebra these are all great ways to go about solving the problem!

Here is the way the author of the problem saw the answer.

Please go back and look at the ways your peers solved the problem. Feel free to post comments, questions, or commend your peers for the way they approached the problem.

If x is the number you think of, you start with x,
Then when you add 1, you get x + 1
When you double it, it turns into 2x + 2
When you take away 3, it turns into 2x -1
Adding the number you first thought of makes 3x -1
When you add 7 it turns into 3x + 6
When you divide by 3 it turns into 1x + 2
Then take away the number you first thought of (x) it leaves 2.

See you Monday,
Ms. Leckman

Welcome to 2007 - 2008 School Year

Well, its a new school year. Part of the class is to participate in the math blog. I will be providing time, probably on Friday's for us to do our posts and a class newsletter. Check this page the first week of school for the problem you will need to work. For now enjoy your summer and I will see you soon!

Ms Leckman