I am elated to see you all saw the need for the Pythagorean Theorem in this problem!
I also noticed many, if not all of you, used guess and check to find the side lengths of your rectangle and this would be fully acceptable - however you never clearly indicated how you knew you had the correct side lengths. There was no proof that they in fact were correct. It was if you magically pulled them out of the air and viol la, they were correct! If you did not, could not explain how you derived your side lengths I docked you points.
I also noticed that the extra credit was not appropriately taken advantage of, and other tasks were undertaken instead. Please do not overlook this opportunity for extra credit in the future.
Ms. L.
All Wet :
A rectangular lawn has an area of 667 square meters.
Surrounding the lawn is a flower border 4 meters wide.
The border alone has an area of 548 square meters.
A circular sprinkler is installed in the middle of the lawn.
What is the spraying radius of the sprinkler if it covers the entire yard, including the flower border?
Explain, in detail, all the reasoning, algebra, and problem-solving techniques you use to solve this problem. Represent all variables and include key steps and formulas you used. Don't forget to include a check for your answer. Answers may be given to the nearest hundredth. Bonus: What percentage of water is wasted (i.e. water that lands outside the lawn and garden)?
Good luck! :-)
667+548=1215
1215 is the total area of the garden.
36 and 33.75
I got these numbers by dividing 1215 by 36 and getting 33.75
Then you cut the rectangle in half to find the circle radius and use the Pythagoras theorem A squared+B squared=C squared. Also subtract it from 8 because that’s the side length of the garden.
(36-8)(33.75-8)
(28)(25.75)
721 squared is 26.85
26.85 is your answer
1215 is the total area of the garden.
36 and 33.75
I got these numbers by dividing 1215 by 36 and getting 33.75
Then you cut the rectangle in half to find the circle radius and use the Pythagoras theorem A squared+B squared=C squared. Also subtract it from 8 because that’s the side length of the garden.
(36-8)(33.75-8)
(28)(25.75)
721 squared is 26.85
26.85 is your answer
Here is BB post:

Here is JS post:
Here is Ms. B.'s (aka frogger) :-)
Here is EK's post:
EMK
667 sq meters is the area of the lawn.
Plus a 548 sq meter border. 4 meters wide.
667+548= 1215 square meters.
Then I thouggght you divided by pi. But you don’t.
The square root of 386.94 (1215/ pi) is ………….. 19.671 which is the raaaaaaaaaaadius
Never mind.
Side Lengths: Length: 22.5 Width: 54. We had help from Tyler and tried different numbers.
54 square root + 22.5= 29.84 would be the radius
667 sq meters is the area of the lawn.
Plus a 548 sq meter border. 4 meters wide.
667+548= 1215 square meters.
Then I thouggght you divided by pi. But you don’t.
The square root of 386.94 (1215/ pi) is ………….. 19.671 which is the raaaaaaaaaaadius
Never mind.
Side Lengths: Length: 22.5 Width: 54. We had help from Tyler and tried different numbers.
54 square root + 22.5= 29.84 would be the radius
First I gathered all the data that was usable:
The Area of the lawn is 667 square meters.
The flower border is 4 meters wide.
The area of the border is 548 square meters.
So, the rectangular lawn has an area of 667 square meters.
The total area of the lawn and garden is 1215. Next you need the sides that equal 34.8568. The Number needed to equal 667 which is the lawn area. I used the process of elimination, until I found two that could be put in the equation and equal 667
The side lengths that I found that worked was 22.5 and 54.
The height of the triangle is 17.4284
You have to cut the rectangle in half to make a triangle. Then you have to use the formula a squared plus b squared equals c squared. That makes a diameter of 58.4. Then you have to cut that number in half to get the radius. The radius is 29.2, which is the sprinkler radius.
The Radius is 29.25
The Area of the lawn is 667 square meters.
The flower border is 4 meters wide.
The area of the border is 548 square meters.
So, the rectangular lawn has an area of 667 square meters.
The total area of the lawn and garden is 1215. Next you need the sides that equal 34.8568. The Number needed to equal 667 which is the lawn area. I used the process of elimination, until I found two that could be put in the equation and equal 667
The side lengths that I found that worked was 22.5 and 54.
The height of the triangle is 17.4284
You have to cut the rectangle in half to make a triangle. Then you have to use the formula a squared plus b squared equals c squared. That makes a diameter of 58.4. Then you have to cut that number in half to get the radius. The radius is 29.2, which is the sprinkler radius.
The Radius is 29.25
Flowerbed area + area of lawn=y
548+667=1215
Side lengths:
Length: 22.5
Width: 54
First, I found the side lengths of the rectangle with the trial and error process. Then I used the Pythagorean Theorem to figure out the radius.
(A squared + B squared= C squared)
54 square root +22.5= 29.25
Answer: 29.25
548+667=1215
Side lengths:
Length: 22.5
Width: 54
First, I found the side lengths of the rectangle with the trial and error process. Then I used the Pythagorean Theorem to figure out the radius.
(A squared + B squared= C squared)
54 square root +22.5= 29.25
Answer: 29.25
And last but not least RB's post:






17 comments:
TG
First I found the total area of the garden and yard which equals 1215 square meters. Next I started by finding the length of each side of the total land mass. I did this by picking a random number to equal 1 side of the land. Then I divided 1215 by that number. This gave me two possible side lengths. The correct border length – 8 times the correct border width-8 equals 667. The 8 came from the 4 meters wide that the border is. So I put the possible side lengths into the equation and that gave me a number which I needed to equal 667 which is the lawn area. I kept trying random number until I found two that could be put in the equation and equal 667. The final side lengths that I found that worked were 22.5 and 54.
Ex. (22.5-8)(54-8)
(16.5)(46)=667
So now I have my side lengths. Now I put the side lengths into the formula of
A squared + B squared = C squared to determine the diameter of the spraying circle. Finally all I had to do was divide the Diameter by 2 gave me my radius.
Final radius= 29.25 square meters.
AM
667
+548
1,215
So we need a circle that can cover that. Hmm.
So now I need to find out the height and width.
LW=667
Hmm.
That’s impossible. So, I need to somehow find the radius. Back to square one.
Square. That’s when it hit me, (thanks to a fellow student.)
I realized, “A square is a rectangle! Thus, since they don’t specify what kind of rectangle, this yard is square to me.”
So now I’m dealing with a square that is 667 m2.
The square root of 667 is…25.83
So each side is 25.83 meters. Plus, a four meter border. That makes it 34.83 wide and long.
Now I need to do Pythagorean theory. A^2+B^2=c^2.
1213.1289
+ 1213.1289
2424.26
The square root of that is 49.3, which is diameter. So 49.3/2= 24.65.
So, the answer is 24.65
JB POW
First I took the areas of the lawn and the flower border and found the square root of them. The square root of 667= 25.82634 and then cut that in half to get 12.913. Then I did the same thing to the area of the flower border to get 11.704. I did this because I cut the lawn and flower border into quarters then made one quarter a triangle. After that I put in the lengths of the sides on the triangle and used the Pythagorean Theorem to get a radius of 24.6.
POW
R.B.
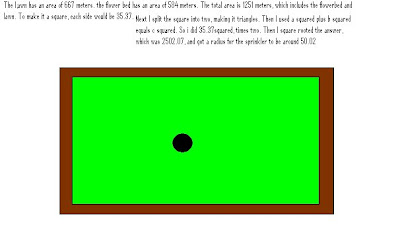
The lawn has an area of 667 meters. The flower bed has an area of 548 meters. The total area of the lawn is 1215, which includes the lawn and flowerbed. The dimensions of this would be 22.5meters by 54 meters. Next I split the square into two pieces, making two triangles. Then I used the Pythagorean Therom. Then 22.5 squared which was 506.25. Also you have to do 54 squared which was 2916.Then I square rooted 3422.25 which is 58.5. This answer is the diameter. So then I divided by 58.5 two and got the circumference of the sprinkler which is 29.25.
POW NH
The area of the lawn plus the area of the flower garden is 1215 which is the total area of the lawn. The flower bed has border of 548 square meters. The rectangular lawn is 667 square meters. 548+ 667 is equal to 1215. 22.5 by 54= lawn + flower bed. Then you have to use the Pythagorean Therom so A= 22.5 and B= 54 and that squared and added together is 3422.25. Square root this and you get 58.5 which is the diameter. Then you divide 58.5 by two to get 29.25 which is the radius.
O. S.
P. O. W.
9/5/08
First of all I added the area of the rectangular lawn with the area of the border. From that I got 1215 square meters. I then knew that if I found the hypotenuse of the rectangle I would find the radius of the circle and then the area of the sprinkler. I figured out the dimensions of the square by dividing 1215 by 22.5 and got 54. The dimensions of the square are now 54 by 22.5. To find the hypotenuse it is a^2 + b^2 = c^2. I then did 22.5^2 + 54^2 = c^2. 22.5^2 is 506.25 and 54^2 is 2916 so 506.25+2916 = 3422.25. Then I had to figure the square root of 3422.25 to find the hypotenuse. The square root of 3422.25 is about 58.5 which is now the hypotenuse. The hypotenuse is also equal to the diameter of the circle. To find the spraying radius of the sprinkler I had to divide the diameter by 2 so I divided 58.5 by 2 and got 29.25. The spraying radius of the sprinkler is 29.25
M.G Pow
All Wet :
A rectangular lawn has an area of 667 square meters.
Surrounding the lawn is a flower border 4 meters wide.
The border alone has an area of 548 square meters.
A circular sprinkler is installed in the middle of the lawn.
What is the spraying radius of the sprinkler if it covers the entire yard, including the flower border?
Explain, in detail, all the reasoning, algebra, and problem-solving techniques you use to solve this problem. Represent all variables and include key steps and formulas you used. Don't forget to include a check for your answer. Answers may be given to the nearest hundredth. Bonus: What percentage of water is wasted (i.e. water that lands outside the lawn and garden)?
Border=548 square meters
Rectangular Lawn= 667 square meters
548+667= 1215 square meters
22.5 by 54 = lawn+ flower box
A= 22.5
B= 54
A squared= 506.25
B squared= 2916
C squared = 3422.25
C= 58.5
Diameter= 58.5
Radius= 29.25
First I found the dimensions that equal 1215 which were 22.5 by 54. The way I found the dimensions were by trial and error. Then I did the Pythagorean Theory to the dimensions and got 506.25 for a squared and 2916 for b squared. I added them together and got c squared 3422.25. To un-square the number and got 58.5. 58.5 would be the diameter of the whole rectangle. To get the radius you divide it by 2 to get 29.25.
Final Radius=29.25
J.K. POW September 12, 2008
All Wet:
A rectangular lawn has an area of 667 square meters.
Surrounding the lawn is a flower border 4 meters wide.
The border alone has an area of 548 square meters.
A circular sprinkler is installed in the middle of the lawn.
What is the spraying radius of the sprinkler if it covers the entire yard, including the flower border?
Explain, in detail, all the reasoning, algebra, and problem-solving techniques you use to solve this problem. Represent all variables and include key steps and formulas you used. Don't forget to include a check for your answer. Answers may be given to the nearest hundredth. Bonus: What percentage of water is wasted (i.e. water that lands outside the lawn and garden)? et:
A rectangular lawn has an area of 667 square meters.
Surrounding the lawn is a flower border 4 meters wide.
The border alone has an area of 548 square meters.
A circular sprinkler is installed in the middle of the lawn.
What is the spraying radius of the sprinkler if it covers the entire yard, including the flower border?
Explain, in detail, all the reasoning, algebra, and problem-solving techniques you use to solve this problem. Represent all variables and include key steps and formulas you used. Don't forget to include a check for your answer. Answers may be given to the nearest hundredth. Bonus: What percentage of water is wasted (i.e. water that lands outside the lawn and garden)?
Lawn= 667 square meters
Flower Border= 548 square meters
667+548=1215 square meters
1215 square meters is the area of the whole lawn, including the flower border that the sprinkler has to spray.
The rectangle is 22.5x54 meters squared I found this out because if you multiply the sides together it equals 1215, the area of the land that the sprinkler had to spray.. Using the Pythagorean Theorem, 22.5 squared = 506.25. The square of 54=2916. Now to find what “C” is in the Pythagorean Theorem, we have to add those two products together and find the square root of the sum. So, 2916+506.25=3422.25. The square root of 3422.25=58.5, the hypotenuse. To find the radius of the hypotenuse “C” which is the radius of the sprinkler’s spray, we have to find half of the hypotenuse’s length. 58.5/2=29.25 meters.
Therefore, the spraying radius of the sprinkler is 29.25 meters!
D.E.
Border= 548 square meters
Rectangular Lawn= 667 square meters
Rectangular Lawn + Border= 1215 square meters
Square Root of 1215= 34.8568 square meters
To find the spraying radius we have to use the Pythagorean Theorem. You find it out by doing A squared by B squared equals C squared. C squared becomes 2429.881. The square root is 49.293 and divide it in half, and then you get the radius of 24.64.
The rectangle is 22.5x54 squared dimensions for the rectangle. If you square 23 you get 529. 55.227x55.227=3050.021. Add these together and you get 3579.227. 22.5 squared is 506.25. The square of 54 is 2916, we’ve found A squared and B squared, C is to add those two together, so that would be 3422.25. The square root of that is 58.5, so then to find the radius of the sprinkler of the garden we divide that by 2 which equals 29.25.
JML
Lawn area is 667 meters squared.
The flower boarder is 4 meters wide.
The boarder alone has 548 altogether.
667+548=1215
Then use the skill of Guessed estimation to figure out the side length.
Length Width
22.5 54
Then you to make up for the corners of the lawn and once you figure that out you have figured out the Radius.
A squared + b squared = c squared
54 square root + 22.5=29.8
MR 9/12/08
At first I made a square to represent the area of the lawn and the border
I uses 1215 (the area of the lawn + the border) then I got the square root of that 34.87
I then used ¼ of the square in order to figure out a radius 17.44 by 17.44 was the area of my “mini” square I then made a line through the middle of my square and used A squared + B squared to get 608.31 square meter
I then found the square root of that to get 24.66 square meters… this is a picture of my work
Later I found out that this was incorrect and used a new strategy which is stated here.
The area of the lawn + the area of the border is 1215 square meters
1215/3.14 Is about equal to 386.94
386.94 squared is about 19.67 meters
The sprinklers spraying radius needs to be 19.67 meters
But that was also incorrect. I tried other methods to find the radius of the circle but none of them were correct.
I tried one last thing and this is it:
1215 divided by 22.5 is 54, the dimensions can be 22.5 by 54, these are correct through a series of trial and error.
54x54=2916
22.5x22.5=506.25
506.25 + 2916=3422.25
Find the square root of this to get 58.5
58.5= the diameter of the circle
58.5/2 = 29.25
The radius of the circle is 29.25
S.S. 9/5/98
Boarder: 548 square meters
Rectangular lawn: 667 square meters
667+548= 1215 square meters
54x22.5=1215
The dimensions of the rectangle is 54x22.5 are the dimensions, 22.5 squared=506.25
The rectangle is 22.5x54. So you do A squared plus B squared= C squared. 23 squared is 506.25. 54x54 is 2916. If you add these together you get 3422.25 the square root of this is 58.5, this is the diameter of where the circle will be placed. So to find the radius we divide the diameter (58.5) by two and you 29.25
The radius of the circle is 29.25.
AM
667
+548
1,215
So we need a circle that can cover that. Hmm.
So now I need to find out the height and width.
LW=667
Hmm.
That’s impossible. There are simply too many answers.
Well, Thanks to a fellow student, I have received information that I must pick to random numbers with trial and error or something to do with the yard area circle stuff.
54x54=2916
22.5x22.5=506.25
Then Add those two. 3422.25
So now I must find the square root! 58.5
Divide by two.
58.5/2= 29.25
So, my answer is 29.25!
MP
667+548= 1215
Find the square root of the square root of both areas. The lawn’s area is square root of 667, which are 25.826. The border area is 548, and the square root of that are about 23.409.
Then you cut 25.826 and 23.409 in half which is 12.913 and 11.705. You do this to make all of the squares into triangles
Then you would take those numbers and put them to a side, so the horizontal lines would be 12.913 and the vertical lines would be 11.705. Then you would use the Pythagorean Theorem to find the measure of the diagonal line, which is also the radius of the circle the diagonal line is (12.913 squared + 11.705 squared) which is about 166.746+137.007 which is 303.753 and the square root of that is about 17.428
Rectangular lawn area is 667 square meters
Flower border is 4 meters wide
Border area is 548 square meters
To find the radius first you
Find the square root of both the areas
Lawn area=667
Square rooted=25.826
Border area= 548
Square rooted= 23.409
Which if you look at the lawn and the border added together to make one square by square rooting the areas you make a smaller square that goes from the center to the corner.
Next you cut 25.826 and 23.409 in half to make the square into two triangles.
25.826/2=12.913
23.409/2=11.705
Then you take the numbers and assign them to a side of the triangle and use the Pythagorean Theorem to find the last side which is the radius if the circle just touches the corner.
12.913*12.913=166.746
11.705*11.705=137.007
166.746+137.007=303.753
303.753 square root is 17.429
C.C.
The rectangular lawn has an area of 667 square meters
The flower border has an area of 548 square meters
Both the border and square areas equal 1215 square meters
In this problem you have to cut the rectangle in half then guess what the bas or height is. I found the random number 54 then I divided 1215 by 54 to get 22.5, which I the height. Then I used the Pythagoras theorem to get 3422.25 then you find the square root of that number which is 58.5 then subtracted by half equals 29.25 which is the radius.
R.H
667
+548
1,215
The sprinkler needs to cover 1,215 square meters.
The area of the rectangle is 667m2. Then I did, though a series of guess and check, 1215⁄22.5 which is 54. So 22.5 and 54 are the detentions of the rectangle. Then you do 22.5x22.5=506.25. Next you multiply 54 and 54 which is 2916. Then you add them together and that is 3422.25. That is the area of the whole rectangle. Next you get the square root of that which is 58.5, which is the length of C. Then you have to divide that by two to get the radius which is 29.25.
Post a Comment