:-) Good luck.
Ms. L.
P.S. Ma ke sure to put both you and your partnership intials in the box you submit your answers. I can't give you credit if I don't know who posted the response. :-)
Here is the POW for this week:
Doug and Anna plan to kayak on the river near their home. The river flows at a rate of 4 miles per hour. In still water they paddle their kayaks at a constant rate of 6 miles per hour. They start and end their trip at the same place on the river. They kayak for exactly two hours, first going upstream and then downstream. What is the total length, in miles, of their trip on the river? Express your answer as a decimal to the nearest hundredth.
You guys did a very nice job this week. Many of you were able to see that the distance there and back needed to be equivalent. The idea of writting them as two equations was a new idea to some of you. Here are two ways to look at the solution to this weeks problem.
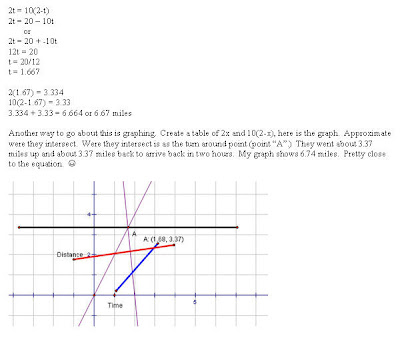
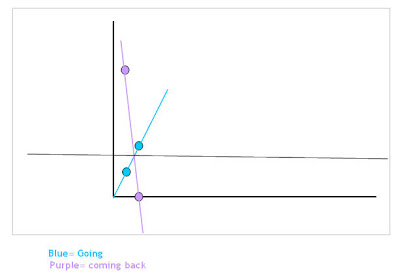
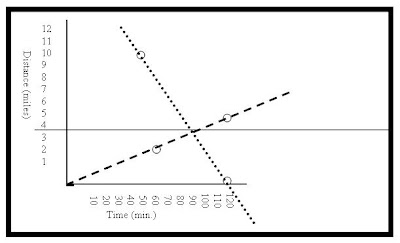
Here are some of your peers graphs and tables. :-)
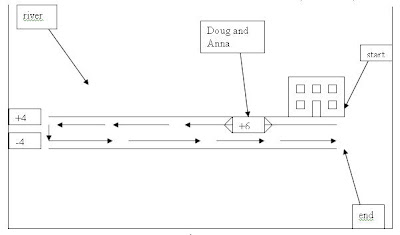


22 comments:
They travel at 10mph going down stream because their kyak travels at 6mph and the river flows at 4mph equaling 10
They travel upsteam at 2mph because their kyak can travel at 6mph but the rivers flowing against them subtracts 4mph making 2mph
so comparing both the fractions:
1/5(fraction)
so if going up stream takes 5 times as long as going downstream then out of 120 mins they spend 20 mins going down stream and 20(5)=100 upstream,
if down stream they go at 10mph and 20mins is one third of that then they travel 3.33 miles going down and up equaling 6.66 miles total
For the first half of their trip they would go 10mph (6+4=10) and then for when they are heading downstream they will go 2mph [6+ (-4)]. The average speed of the kayaks is 6mph (2+10=12/2=6). So the 2hours multiplied by the 6miles per hour average speed pf the kayak will give the total length of the river, 2*6=12 miles. The river is 12 miles long.
IW
Equation 1: [Upstream]
60/4=?
60/4=15
15(x)=?
15(x)=72.5
Equation 2: [DownStream]
60/6=?
60/6=10
10(x)=?
10(x)=47.5
To get 72.5 and 47.5 we started with 5 miles up and 5 miles back. But to do that there would be 5 minutes over the 2 hours, so we had to take 5 minutes off. We reduced 50 to 47.5 and 75 to 72.5 which would take 5 minutes off the total time making there trip 2 hours exactly.
Then we had to find what "X" could be in both the equations to make the equations into solutions.
We divided 72.5 by 15, and 47.5 by 10. And got 4.83.
Altogether they traveled 9.66 miles.
CK, VB, AR, JS, & CT
Doug and Anna plan to kayak on the river near their home. The river flows at a rate of 4 miles per hour. In still water they paddle their kayaks at a constant rate of 6 miles per hour. They start and end their trip at the same place on the river. They kayak for exactly two hours, first going upstream and then downstream. What is the total length, in miles, of their trip on the river? Express your answer as a decimal to the nearest hundredth.
When they travel downstream with the current, they travel at 10 mph. (6+4=10) Next when they head upstream, they will be traveling at two mph, because they paddle faster than the river flows. (6-4=2) If they travel 4 miles down stream it would take 24 minutes, to get back upstream, 4 miles, it would take them 120 minutes. 24+120=144. 144 minutes is more than two hour, because two hours is 120 minutes. If they travel 3 miles, it would take them 18 minutes, it would then take them 90 minutes to get back. 18+90=108. 108 minutes is 12 minutes less than 120 minutes. If they traveled about 3.5 miles it would take them 21 minutes, and 105 minutes to get back upstream. 21+105=126. They traveled approximately 3.5 miles both up and down stream. Combined they traveled about 7 miles.
A.L. and E.Mu.
K.A. C.V.D.
V
If they travel downstream at 6 minutes per mile and upstream 30 minutes per mile the equation is 30x+6x=120. Now all we got to do is plug in the exact number for “x” and we are done. X=3.333 they traveled at 3.33 miles per minute to get there and back to the same place they started.
The problem we were given was that we had to figure out what the total length in miles of Doug and Anna's trip on the river. We had to express our answer in a decimal to the nearest hundredth. The total miles on the river were 10 miles. We deduced this because we decided to put it into two different equations, one for going up and one for going down the river. We decided that the equation for going up was, 4x=? The equation for going down was 6x=?. We knew that the trip only lasted for a total of two hours. If it was two hours than it should be safe to add 1 in the "x" variable in the equations. When that was done we added those together and got 10 miles. If it was 10 miles, you can't go up 4 and down 6! So we had to make it even and 10 divided by 2 was 5. After we got 5 we had to turn it into a fraction and find common denominators. We then turned 6/6 and 4/4 into 12/12 and 12/12. After that we turned 12/12 into 9/12 and 12/12 into 15/12 and then we turned 9/12 into a decimal which was .75 and 15/12 in a decimal 1.25. So, 1.25 plus .75 is an even 2. It took 80 minutes to go up and 40 minutes to go down.
M.G.
R.S.
D.M
They travel 26 miles, because going upstream they can only travel about 2 miles because the water is coming towars them at 4 m.p.h. and then going down river they travel 4 times faster so it equals about 26 miles.
J.B.
P.O.W.
C.J.H.
Here is the POW for this week:
Doug and Anna plan to kayak on the river near their home. The river flows at a rate of 4 miles per hour. In still water they paddle their kayaks at a constant rate of 6 miles per hour. They start and end their trip at the same place on the river. They kayak for exactly two hours, first going upstream and then downstream. What is the total length, in miles, of their trip on the river? Express your answer as a decimal to the nearest hundredth.
If the water is flowing at 4 MPH then if they kayak at 6 MPH in still water, then going downstream they will go 10 MPH. They are out for 2 hours first going upstream. When kayaking against the flow of the river they are going 2 MPH. If they go upstream for 1 hour and 40 minutes they get 3.33 miles, when they downstream they will get 3.33 miles in 20 minutes going ten miles an hour. When they arrive at their starting point they will have gone
6.66 miles.
C.J.H.
P.O.W.
D. E.
Doug and Anna plan to kayak on the river near their home. The river flows at a rate of 4 miles per hour. In still water they paddle their kayaks at a constant rate of 6 miles per hour. They start and end their trip at the same place on the river. They kayak for exactly two hours, first going upstream and then downstream. What is the total length, in miles, of their trip on the river? Express your answer as a decimal to the nearest hundredth.
The river flows at a rate of 4 miles per hour, and the kayaks ride at a rate of 6 miles per hour. They start where they finish, so they do not continue. They first have to go upstream, which will make the water go towards them, making the 6 miles per hour to 2 miles per hour, because of the pressure of going upstream, the water pushes at them. Then when they go downstream, they add 4+6 which would make a faster rate of 10 miles per hour. So they first do upstream, which is making them go 2 miles per hour. When they go upstream for 1 hour and 40 minutes they get 3.33 miles, when they go downstream they will get 3.33 miles in 20 minutes going 10 miles an hour. When they arrive at their starting point they will have gone 6.66 miles.
P.O.W.
M.R
Doug and Anna plan to kayak on the river near their home. The river flows at a rate of 4 miles per hour. In still water they paddle their kayaks at a constant rate of 6 miles per hour. They start and end their trip at the same place on the river. They kayak for exactly two hours, first going upstream and then downstream. What is the total length, in miles, of their trip on the river? Express your answer as a decimal to the nearest hundredth.
The river flows up at a rate of 4 miles per hour the kayaks at 6 mph. They first have to go upstream going 6mph subtracted by 4 mph from the river is 2 mph going up stream and 6+4 mph going down stream is 10 mph. so that is 2 mph in the first part and 10 mph in the second
So for 1 hour and 30 minutes they go 3 miles up but going down they go 10 mph so in 30 minutes they went 5 miles in
In 1 hour and 40 minutes they went 3.33 miles up and in 20 minutes they go down 3.33 mph because 10/3 = 3 and 1/3
answer:In total they go 6 and 2/3 miles
They travel at 4 miles per hour without paddling because of the flow of the stream. They travel at a rate of 6 miles per hour on still water. If they paddle at 6 miles per hour while traveling 4 miles per hour with the current, they travel a total of 10 miles per hour. First they travel upstream at a rate of 2 miles per hour.
time Far going Distance
coming
30 1` 5
1 2 10
1.5 3 15
2 4 20
AH BB
When they are going upstream, they are paddling at 6 miles an hour, but the stream is going against them at 4 miles an hour so they would have gone 2 miles upstream.
When they are going downstream, they are paddling at 6 miles an hour, but since they are going down stream at 4 miles an hour, they would have gone 10 miles downstream. In total, they would have gone 12.00 miles in 2 hours.
O. S. and C. H. C.
P.O.W.
C.J.H.
Here is the POW for this week:
Doug and Anna plan to kayak on the river near their home. The river flows at a rate of 4 miles per hour. In still water they paddle their kayaks at a constant rate of 6 miles per hour. They start and end their trip at the same place on the river. They kayak for exactly two hours, first going upstream and then downstream. What is the total length, in miles, of their trip on the river? Express your answer as a decimal to the nearest hundredth.
If the water is flowing at 4 MPH then if they kayak at 6 MPH in still water, then going downstream they will go 10 MPH. They are out for 2 hours first going upstream. When kayaking against the flow of the river they are going 2 MPH. If they go upstream for 1 hour and 40 minutes they get 3.33 miles, when they downstream they will get 3.33 miles in 20 minutes going ten miles an hour. When they arrive at their starting point they will have gone 6.66 miles.
P.O.W.
D E
Doug and Anna plan to kayak on the river near their home. The river flows at a rate of 4 miles per hour. In still water they paddle their kayaks at a constant rate of 6 miles per hour. They start and end their trip at the same place on the river. They kayak for exactly two hours, first going upstream and then downstream. What is the total length, in miles, of their trip on the river? Express your answer as a decimal to the nearest hundredth.
The river flows at a rate of 4 miles per hour, and the kayaks ride at a rate of 6 miles per hour. They start where they finish, so they do not continue. They first have to go upstream, which will make the water go towards them, making the 6 miles per hour to 2 miles per hour, because of the pressure of going upstream, the water pushes at them. Then when they go downstream, they add 4+6 which would make a faster rate of 10 miles per hour. So they first do upstream, which is making them go 2 miles per hour. When they go upstream for 1 hour and 40 minutes they get 3.33 miles, when they go downstream they will get 3.33 miles in 20 minutes going 10 miles an hour. When they arrive at their starting point they will have gone 6.66 miles.
Here is the POW for this week:
Doug and Anna plan to kayak on the river near their home. The river flows at a rate of 4 miles per hour. In still water they paddle their kayaks at a constant rate of 6 miles per hour. They start and end their trip at the same place on the river. They kayak for exactly two hours, first going upstream and then downstream. What is the total length, in miles, of their trip on the river? Express your answer as a decimal to the nearest hundredth.
12.00 miles because when they go up stream for a hour moving six miles per hour minus four mile since their moving against the river they moved 2 miles, when they moved with the river their pace increased from six to ten miles per hour because the river current moves four miles per hour by itself.
C.H.C. and O.S.
They go 10mph at a constant rate downhill. (6+4=10)
When going uphill they go only 2mph, they are paddling at 6 mph but the current of the water is pushing against them at 4mph. (6-4=2).
At first they’re going 2mp for the first hour, then for the next hour they’re going 10mph.
H.R.
So when you’re going downstream you are going 10 miles because you’re adding the river flow and the kayaks flow. If you’re going upstream you’re only going 2 miles per hour because you subtract the kayak flow by the river flow.
S.M.
They go 10 mph constant on regular water or down hill; they go mph going up stream so at first they go two mph for one hour so they go two mile for the first hour. Then they go 10 mph and travel for another 10 miles.
They go 0.033333 Miles per minute while going up hill
Then going down hill they go 0.16667 Miles per hour while going down the river. They go it takes them longer going upstream. So they go for about 1 hour 40 minutes upstream because it is 4/5 longer 2/10 is 4/5 So for 1 hour 40 minutes they go 3.333 and for the last 20 minutes they go 1/3 of an hour so that is another 3.333 miles, that times 3 is the 10 miles per hour, so in total it is 6.6 Miles is the total length of the river.
S.S. and J.K.
(4+6)x downstream x=number of hours
(6-4)x going upstream
3.5 .35
3.3 1.65
3.4 .34
3.33 .333
1.66
(4+6) (.33)
(10) .33=?
(10) .33=3.33 they kayak for 20 minutes at a rate of 10 miles an hour
(6-4) (1.66)
(2) 1.66=?
(2) 1.66=3.33 they kayak for 1 hour and 40 minutes at a rate of 2 miles an hour
Doug and Anna are going to kayak on the river by there home. The river flows at a rate of 4 mph. They also are going to paddle the bout and a constant rate at 6 mph. They travel for exactly 2 hours first up stream then down stream. You would be going 3.5 miles upstream and then 3.5 miles down stream.
D.C. and K.G.
P.O.W.
M. R.
Doug and Anna plan to kayak on the river near their home. The river flows at a rate of 4 miles per hour. In still water they paddle their kayaks at a constant rate of 6 miles per hour. They start and end their trip at the same place on the river. They kayak for exactly two hours, first going upstream and then downstream. What is the total length, in miles, of their trip on the river? Express your answer as a decimal to the nearest hundredth.
The river flows up at a rate of 4 miles per hour the kayaks at 6 mph. They first have to go upstream going 6mph subtracted by 4 mph from the river is 2 mph going up stream and 6+4 mph going down stream is 10 mph. so that is 2 mph in the first part and 10 mph in the second
So for 1 hour and 30 minutes they go 3 miles up but going down they go 10 mph so in 30 minutes they went 5 miles in
In 1 hour and 40 minutes they went 3.33 miles up and in 20 minutes they go down 3.33 mph because 10/3 = 3 and 1/3
answer: In total they go 6 and 2/3 miles
Post a Comment