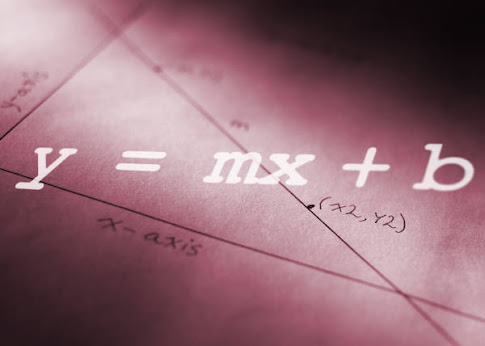Please click on the school year 2009-2010 and we will be off and running! See the link below or in the navagation sidebar. ;-)
Thursday, August 20, 2009
Thursday, April 16, 2009
Final Project - Creating a Lesson for Others
Ms. L.
Our Web Page
Friday, December 12, 2008
Holidays are here!
The first is the most important and is required. You will determine how much it would cost to purchase all the items in the song, The Twelve Days of Christmas. Go to the following site to find the unit cost of each of the items in the song. Then determine how much it would cost in total, for all the items. Here is a site that will tell you this years costs for these items:
http://www.pncchristmaspriceindex.com/CPI/index.html
A couple of tips:

You may want to use excel to help in this task.
If you use excel save it and send it to our mathclasshonors@yahoo.com mailbox (include your name!!!) and I will give you extra credit!
BIG, BIG, BIG!!!! Remember that you that you will be purchasing a partidge in a pear tree on the first day, but on the second day of christmas you buy two turtle but you buy another partidge in a pear tree.
Task Two - Extra Credit:
Develope your own Twelve Days of Christmas. Create a list of what you would buy your "True Love" on the Twelve Days of Christmas and find out what it would cost you for these items. REMEMBER: If you buy, one the first day of Christmas the Batman the Dark Night, then for the second day you buy, Guitar Hero you have to buy them another Batman the Dark Night.
Task Three: This one is also extra credit.
Here is a list of online snowflake makers. (They are very fun, I tried each one myself!) You may play on the sites. Make some snowflakes. When you have made one you really like download or copy it, and then print it.
http://snowflakes.barkleyus.com/
http://www.zefrank.com/snowflake/
http://www.popularfront.com/snowdays/
http://gwydir.demon.co.uk/jo/symmetry/snow.htm
http://compute2.shodor.org/cgi-bin/snowflake/snowflake.pl
Now make a list of all the geometric properties and attributes contained in the snowflake. You may want to do a bit of research on snowflakes to find some of these properties. This is the important part and this is where I will determine the value of the extra credit. The snowflake itself is worth no extra credit points!
Have fun!
Ms. Leckman
P.S. The extra credit is due Monday!
Sunday, August 31, 2008
Wet and Wild
Ms. L.
Thursday, August 28, 2008
All Wet
I am elated to see you all saw the need for the Pythagorean Theorem in this problem!
I also noticed many, if not all of you, used guess and check to find the side lengths of your rectangle and this would be fully acceptable - however you never clearly indicated how you knew you had the correct side lengths. There was no proof that they in fact were correct. It was if you magically pulled them out of the air and viol la, they were correct! If you did not, could not explain how you derived your side lengths I docked you points.
I also noticed that the extra credit was not appropriately taken advantage of, and other tasks were undertaken instead. Please do not overlook this opportunity for extra credit in the future.
Ms. L.
All Wet :
A rectangular lawn has an area of 667 square meters.
Surrounding the lawn is a flower border 4 meters wide.
The border alone has an area of 548 square meters.
A circular sprinkler is installed in the middle of the lawn.
What is the spraying radius of the sprinkler if it covers the entire yard, including the flower border?
Explain, in detail, all the reasoning, algebra, and problem-solving techniques you use to solve this problem. Represent all variables and include key steps and formulas you used. Don't forget to include a check for your answer. Answers may be given to the nearest hundredth. Bonus: What percentage of water is wasted (i.e. water that lands outside the lawn and garden)?
Good luck! :-)
1215 is the total area of the garden.
36 and 33.75
I got these numbers by dividing 1215 by 36 and getting 33.75
Then you cut the rectangle in half to find the circle radius and use the Pythagoras theorem A squared+B squared=C squared. Also subtract it from 8 because that’s the side length of the garden.
(36-8)(33.75-8)
(28)(25.75)
721 squared is 26.85
26.85 is your answer
Here is BB post:

667 sq meters is the area of the lawn.
Plus a 548 sq meter border. 4 meters wide.
667+548= 1215 square meters.
Then I thouggght you divided by pi. But you don’t.
The square root of 386.94 (1215/ pi) is ………….. 19.671 which is the raaaaaaaaaaadius
Never mind.
Side Lengths: Length: 22.5 Width: 54. We had help from Tyler and tried different numbers.
54 square root + 22.5= 29.84 would be the radius
The Area of the lawn is 667 square meters.
The flower border is 4 meters wide.
The area of the border is 548 square meters.
So, the rectangular lawn has an area of 667 square meters.
The total area of the lawn and garden is 1215. Next you need the sides that equal 34.8568. The Number needed to equal 667 which is the lawn area. I used the process of elimination, until I found two that could be put in the equation and equal 667
The side lengths that I found that worked was 22.5 and 54.
The height of the triangle is 17.4284
You have to cut the rectangle in half to make a triangle. Then you have to use the formula a squared plus b squared equals c squared. That makes a diameter of 58.4. Then you have to cut that number in half to get the radius. The radius is 29.2, which is the sprinkler radius.
The Radius is 29.25
548+667=1215
Side lengths:
Length: 22.5
Width: 54
First, I found the side lengths of the rectangle with the trial and error process. Then I used the Pythagorean Theorem to figure out the radius.
(A squared + B squared= C squared)
54 square root +22.5= 29.25
Answer: 29.25
And last but not least RB's post:
Happy First Friday
There are some ground rules for those of you that are new to Friday Math Lab.
1. You are here to do math.
2. You come into the lab, log in, and proceed to the Problem of the Week (POW) for your class.
3. POW's are a requirement of the class. It is an assignment and it is graded.
4. You may work with a partner, however the final post needs to be in your own words. (Everyone needs a post so I can give you a grade.)
5. You may use any resources you need on the web, in the book, or with each other to post your solution.
6. All post automatically go to me prior to the web. I will approve it for the web. I will let you know when I have accepted and posted your work. However, keep in mind that I can call you up and tell you it is not finished and you will need to go back and edit your work.
7. Keep in mind from where I sit, I see all of your screens. :-)
8. You must start your post with the intial of your first name and your last name. NEVER USE A WHOLE NAME, NEVER REFER TO ANYONE IN THE CLASS USING A FULL NAME. You may use my whole name.
TIPS:
1. Work in Word first and then cut and paste to the comment box. If you leave the comment box open too long you will lose all of your work. (Also, you can not copy from the comment box and paste in Word. See why this is important in the next bullet.)
2. Always save your work in the Leckman to be graded file. If for some reason your post is lost while you are submitting it, we still have a copy.
3. Use appropriate language, we are live for everyone to see. You are the image of Madison Number One through your voice on the web.
Now on to your task for today:
7th Grade Honors - please read through: Tips for the New 7th Grade AEP, from last years 7th grade. Post your thoughts on their tips and then proceed to the 7th grade page and begin your POW.
8th Grade - Proceed to the 8th Grade page and begin your POW.
Welcome back 8th Honors - Here ya go... You get a choice today. I have a page set up for you if you would like a seperate page or you can keep posting on this page. I am rather proud of your work here and would love to see you stay here, but it is totally your choice. We need to decide which way we want to go. We will proceed from there. :-)
Good luck to all.
Ms. L.
Wednesday, May 28, 2008
Tips for the "new" 7th grade AEP!
Then provide a name, either you or one of your peers to organize the data (tips) and reorganize it in a manner that will be meaningful for our new group.
thx,
Ms. Leckman
Friday, May 02, 2008
Re-visit Function This Function That
 Ms. Leckman
Ms. Leckman8th Grade POW
IMPORTANT!!! Be careful, some of the 7th grade questions ask for names - I WILL NOT POST WITH TEACHERS NAMES OR INTIALS. However you may discuss tough content areas and how to make themselves and their teachers happy to ensure a success and or pleasant 8th grade year. :-)
Here is your second task:
Think of a function as a math machine with an input and an output. Suppose the function is A(x) = 3x + 1. That means if you put any number (x) into this function machine, the machine will multiply the number by three and add one. For example, what is the output if five is the input? Five times three plus one equals 16 for the output. That's written A(5) = 16.
Suppose you join two function machines so that the output of the first one is connected to the input of the second one. Let's make the second function B(x) = x^2, (remember that x^2 means x squared). If you put two into the A machine, out comes seven. Then seven is the input to the B machine which squares it, and out comes 49. Okay? That's written B(A(2)) = 49.
Here are five functions:
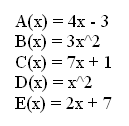
I am going to connect them in alphabetical order and use two as the input number. That would be written as E(D(C(B(A(2))))). The resulting output = 553,359.
What arrangement of functions will produce the largest output? Let x = 2 (or your input.) Each function used only once. I am looking for logical reasoning and algebra rather than just guess and check. Explain why you chose your particular arrangement. (Make sure to include your function in well formed, symbolic notation.)
7th Grade POW
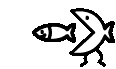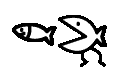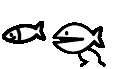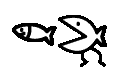
Ms. Leckman decided that the Math Club mascots, Fibonacci and Descartes, had outgrown their 10-gallon home, so this weekend she picked up a 15-gallon aquarium at a flea market. Oliver and Suzanne have been assigned the task of setting up the new aquarium. They have been instructed to fill it exactly three-quarters of the way to the top. Fibonacci and Descartes will be transferred with some of the water from their current environment to help them adjust to their new home. Unfortunately, Suzanne and Oliver can not find a clean bucket for carrying water to the aquarium. All they can find are two eight-ounce glasses. Working from the sink to the left of the aquarium stand, Suzanne takes 45 seconds to fill one glass and dump it into the aquarium. Working from the sink to the right of the aquarium, Oliver can fill one glass and dump it into the tank in 39 seconds.
If Suzanne and Oliver start at noon and keep working at these constant rates, what time will they complete their task? Which student will add the last glass of water?
Friday, April 25, 2008
Asking 8th Graders
Question one needs to be regarding success in the 8th grade.
Question two needs to be regarding 8th grade Honors Math class.
And the final question is anything you want.
Make sure that no one has asked any of your questions. Each question needs to be unique.
Ms. Leckman
Friday, April 11, 2008
Welcome back!!!!!!!!!!
Today you will be completing two tasks. The first task is to present your perspective on AIMS assessments. The second is a math problem. Be sure to fully explain your answer, that means show how you got your answer. If you use symbolic notation understand that an equation is a tool to support proof. Explain what each of the parts of your equation represent and why they are important or why you have considered these factors.
PART 1
Here are questions I would like you to address:
1. Do you like AIMS?
2. Does AIMS show what you personally know?
3. If you wanted to demonstrate what you have learned this year - how would you go about
proving your new mathematical understandings?
PART 2 - THE PROBLEM
Saturday, March 29, 2008
Bye Bye Blog
Friday, March 14, 2008
Math without Mathematicians?
Although we engage in learning mathematics every day, we never stop to think about the fact someone actually took the time to figure out the structures, connections, and rules of mathematics so that we could use it without having to re-figure it out every time. Here is your task for the day. Follow these links for historical information:
http://www.agnesscott.edu/Lriddle/women/women.htm
http://www-groups.dcs.st-and.ac.uk/~history/index.html
http://www-groups.dcs.st-and.ac.uk/~history/BiogIndex.html
http://math.about.com/od/mathematicians/Mathematicians.htm
Explore some of the mathematicians or the mathematicians related to a genre of mathematics. Give us a peak into the world of three mathematicians. Be sure you understand what it is they really contributed to mathematics before you post. (This is why you may want to search by topic.)
In your write up please include the following:
Name
Era
Branch of mathematics
A interesting fact about the mathematician
How their contribution helps us today, give a real life example of the mathematics, or explain How their contribution has shown up in our studies.
You may not cut and paste. These are written in your own words in paragraph form, including correct spelling and puncuation. I can't wait to read what you find out about the eclectic world of mathematicians.
Ms. Leckman
P.S. Don't forget to make a major and minor edit to the wiki.
ENJOY YOUR BREAK!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
SEE YA IN 9 DAYS. :-)
Friday, March 07, 2008
How Did They Know?????

Friday, February 29, 2008
And now for something completely different
http://muchadoaboutmath.wetpaint.com/
Today we will also be looking at what you know and what you do not know. Today will provide a way for you to know what to practice prior to our Benchmarks and AIMS. Please follow the links to the practice tests. These test will provide feedback for you immediately so you have an idea where your strengths and refinement areas lie.
When you find your refinement area you can use your books or the online activities and 'How to's' to improve your understandings.
McDougal Littell
http://www.classzone.com/books/algebra_1/index.cfm
MAC 8th Grade
http://www.glencoe.com/sec/math/msmath/mac04/course3/index.php/az/2004
MAC 7th Grade
http://www.glencoe.com/sec/math/msmath/mac04/course2/index.php/az/2004
Please print the scores to your section assessments and bring them to me. Make sure your names on them.
Please let me know if you need any assistance.
Ms. L.
Friday, February 15, 2008
Pool Tables
Marisa created a game called Paper Pool. Her pool tables were rectangles drawn on grid paper. The pockets at each corner were labeled A (lower left), B (lower right), C (upper right), and D (upper left). Marisa described each table by its size, giving the horizontal length first and the vertical height second. The figure below shows a 6 × 4 table.

How to Play Paper Pool
• The lower-left corner is always corner A, and the labeling continues counterclockwise
with B, C, and D.
• The ball always starts in corner A.
• The ball is hit with an imaginary cue (a stick for hitting a pool ball) so that it travels at a
45° diagonal across the grid.
• If the ball hits a side of the table, it bounces off at a 45° angle and continues its travel.
• The ball continues to travel until it hits a pocket.
Link to webpage:
http://illuminations.nctm.org/ActivityDetail.aspx?ID=28
Link to handouts:
http://juliesgotmail.googlepages.com/home
Questions:
1. In what corner will the ball stop?
2. How many hits will have occurred by the time the ball stops?
3. Write rules (equations) that you could use to determine what will happen to the ball as it travels on a table of any size. Your rules (equations) should tell you, without drawing the path, the corner at which the ball will stop and the number of hits that occurred. (These might be separate equations.)
Support your answers with examples in the form of patterns, spreadsheets, tables, graphs and or illustrations.
If you have any questions please see me.
Ms. Leckman
Here is a short video with some of your responses. My video will go fast so be prepared to use the pause button to spend a minute or two on a solution. I will be posting these on our class webpages to see if we can get a larger view. :-)
K.A. Video
Enjoy. I will try to post more video this year. :-) Yes, I truly am a nerd, I try to learn new "stuff" (sorry Mrs. Campbell) all the time. :-)
Ms. L.
Friday, February 01, 2008
Star Light Star Bright
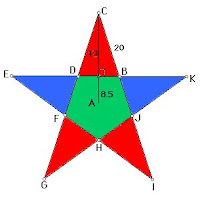
Martha Stewart wants to rebuild her ugly garden. She thinks it needs a modern twist and decides to make a star-shaped garden where the legs of the star will be filled with flowers and the central pentagon will be grass.
Martha needs your help to calculate the floral area and grassy area in this new garden design. Then she can figure out the equipment and materials she will need for the project.
To form this star, simply extend the sides of the pentagon to make the legs of the star. Here are the dimensions of her stellar garden:
each leg of the star is a triangle with two sides, both 20 feet long, and an height of 19 feet.
The pentagon is regular (the sides are all equal and the angles are all equal),
and the distance from the center of the pentagon to one of the sides is 8.5 feet.
To the nearest square foot, what are the areas of Martha's flower section and grass section. Because Martha is not sure what she would like to do, please provide three different ways she could arrange her garden, be sure to let her know the area each floral and grass area will take. Explain how you solved one of the area problems. BE SPECIFIC! Walk us through all of your steps.
HERE ARE SOME OF YOUR SOLUTIONS:
What are the odds????

Friday, December 07, 2007
POW Dec 3

Nice job guys! Many of you not only found the correct answer but were moving towards the correct algrithm. Here is the answer for this weeks blog. have a great weekend!
Ms. L.
Correct answer:7 kids * 2 legs = 14 legs
7 kids * 7 rucksacks = 49 rucksacks
49 rucksacks * 7 big cats * 4 legs = 1,372
legs49 rucksacks * 7 big cats * 7 small cats * 4 legs = 9,604
legs14 + 1,372 + 9,604 = 10,990 legs total.
This may also be shown as a simple powers of 7 problem:
Total legs = 7^1 * 2 + 7^2 * 0 + 7^3 * 4 + 7^4 * 4. This is because there are:7^1 * 2 kids legs7^2 rucksacks (But they don't have legs)7^3 * 4 big cat legs7^4 * 4 small cat legsOf course, 7^2 * 0 could be omitted completely, but I include it just to show the progression of powers of 7.
Friday, November 30, 2007
7th Grade Nov. 26th
A banana farmer has six monkeys who hate each other. They must be kept in pens to separate them from the bananas as well as from each other.
The farmer has created six pens of equal size using 13 equal lengths of fencing. The pens are organized in a row.


How can the farmer reorganize the fencing to make six new pens of equal size with the 12 remaining lengths of fencing?
Have fun. Remember to back up your document in the TO BE GRADED file and submit your responses to:
Ms. Leckman
Thursday, November 15, 2007
7th and 8th Grade POW Nov. 12th
I have a number of post from the 7th Grade class that have no names. :-( If one of the POWs is yours and there is no name on it you MUST see me. Mid terms are coming out if you want credit for this POW, see me before the break!!!
P.S. See below for further submission check out the final submission!
Good Luck with the problem.
Ms. L.
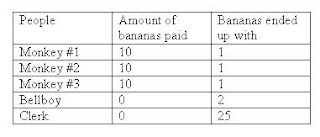
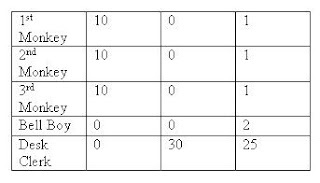
Three monkeys walk into a motel on the Planet of the Apes and ask for a room. The desk clerk says a room costs 30 bananas, so each monkey pays 10 bananas towards the cost.
Later, the clerk realizes he made a mistake, that the room should have been 25 bananas. He calls the bellboy over and asks him to refund the other 5 bananas to the 3 monkeys. The bellboy, not wanting to make a mess dividing the 5 bananas three ways, decides to lie about the price, refunding each monkey 1 banana, keeping the other 2 bananas for himself. Ultimately each monkey paid 9 bananas towards the room and the bellboy got 2 bananas, for a total of 29 bananas. But the original charge was 30 bananas.
Where did the extra 1 banana go?
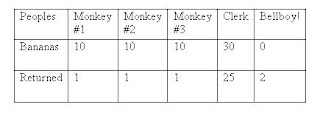
When the monkeys entered they paid the fee of 30 bananas, but the clerk made a mistake and it was 25 bananas so he gave the 5 bananas to the bellboy to give back evenly. But he didn’t, to make it easier on himself he decided to give 1 to each monkey and keep the two to himself.
So when I plotted on the table missing bananas, you find out if you add it up you find there was no missing banana! ~!!YAY!!~
The equation is 29=9x3+2
By AH

Friday, November 09, 2007
8th Grade POW Nov. 5th
The problem this week is an old one, in fact over 500 years old. It goes back to the days in Europe when fairs were common in many cities, and merchants would travel from city to city, selling their various goods and buying other items they desired.
It seems that a humble merchant visited three fairs. At the first fair, early in the morning, he doubled his money selling his products, but spent $30 in food and buying other items.
At midday at the second fair, he tripled his money and spent $54. At the third fair in the afternoon he quadrupled his money but spent $72.
Upon his return home to his wife and ten children, late that day, he counted the money he had in his bag; there was $48.
 Now, if the merchant returned home with a profit his wife was happy and she was sad if he returned home with less money than when he started with. So tell me: was his wife happy or sad when he returned? And how much did the man gain or lose, respectively?
Now, if the merchant returned home with a profit his wife was happy and she was sad if he returned home with less money than when he started with. So tell me: was his wife happy or sad when he returned? And how much did the man gain or lose, respectively?Remember: although this type of problem could be solved by guess-&-check or reverse analysis, such an approach will not be accepted here. (You may use them separately to verify your answer; however substitution would be the best way to check your answer.) You must construct an equation for credit. Make sure to label the steps for your solution.
Extra Credit (this is very easy this week don’t over look the opportunity!): If you did your work straightforwardly, your next-to-last step of equation work was of the form (m) x = n. The number “n” is in some way rather interesting; what is it?
Extra Credit: The next-to-last step is where Ax=B (24m=696) is interesting because B (696) is a palindrome. If you do not know what a palindrome is please look it up, it is not just a Language Arts phenomenon. :-)
Monday, November 05, 2007
7th Grade POW for November 5th
 Ann and Sue bought identical boxes of stationery. Ann used hers to write one sheet letters, and Sue used hers to write three sheet letters. Ann used all the envelopes and had 50 sheets of paper left, while Sue used all of the sheets of paper and had 50 envelopes left. How many sheets of paper and how many envelopes were in the box to begin with?
Ann and Sue bought identical boxes of stationery. Ann used hers to write one sheet letters, and Sue used hers to write three sheet letters. Ann used all the envelopes and had 50 sheets of paper left, while Sue used all of the sheets of paper and had 50 envelopes left. How many sheets of paper and how many envelopes were in the box to begin with?Make sure to thoroughly explain how you solved the problem. Show your mathematics and explain as you go so we understand what the numbers are and where you got them or why they are important.
Good luck,
Ms. L.
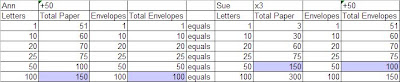
To begin the problem you had to account for the proportions or ratios of items to solve the problem. Anne used one piece of paper per letter and Sue used three pieces of paper per letter. If you thought about the number of materials per letter you could set up a table of paper and envelopes per letter. Doing so you would want to add 50 to the number of papers Anne used because she had fifty left over, and you would want to add 50 to Sue’s envelopes as she had 50 envelopes left over. Then all you needed to do was test various numbers of letters, and continue until the total paper and total envelopes were the same for both girls.
Here is the table I made. You can see from the table the girls started with 150 pieces of paper and 100 envelopes.
Here is another table done by AH:
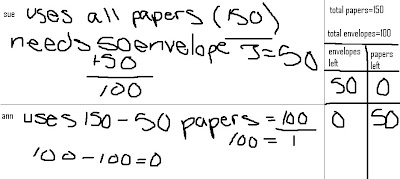
Trying to find the best way
I have begun reading your posts for last week. I am trying to determine the best way to post these. I may begin a website just for the postings that tend to be multi-media. Give me a couple days to figure this out, I will keep you posted in class.
ms.l.
Saturday, October 27, 2007
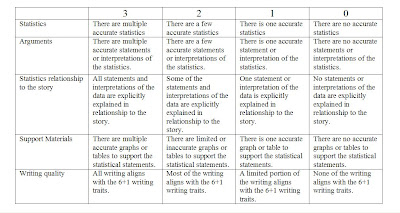
Rubric for the To Kill a Mockingbird Blog response
Monday, October 22, 2007
POW Oct 22 - California Wildfires
 I had a seasonal POW set and ready to go, however I think the fires in California might be of more importance right now. Here is what I would like from you. I would like you to read up a bit about the fires. Look for some of the math in the web articles, on the news, and in the newspaper. See what kind of mathematical information you can share with us to make this a bit easier to understand. Think back to our 9/11 comparisons. For example I could write and post something like.
I had a seasonal POW set and ready to go, however I think the fires in California might be of more importance right now. Here is what I would like from you. I would like you to read up a bit about the fires. Look for some of the math in the web articles, on the news, and in the newspaper. See what kind of mathematical information you can share with us to make this a bit easier to understand. Think back to our 9/11 comparisons. For example I could write and post something like.300,000 people have been evacuated from their homes as of today. To understand how many people that is we can compare them to the population of Phoenix. Currently there are 1.512,986 people who reside in Phoenix. This would be the same as evacuating 20 percent or 1/5th of Phoenix.
There are many comparisons you can make
Acres burned
Number of houses destroyed
Area of land affected by wildfires
Number of fireman engaged in fighting the fires
Comparisons to the Rodeo Chediski fires
You need to make at least three comparisons and then write a narrative using your comparisons. Adhere to the 6 plus 1 writing traits. I will be grading on math content, impact of the data through your writing, and mathematical support for your comparisons, graphs, tables etc.
Here are some websites to get you started. I will add to the list as I find good ones, however you will need to find some sites as well. Remember to credit any sites you use for your data or information such as maps or statistics. I will be posting a PowerPoint presentation on the 7th grade website tomorrow evening.
Ms. L.
Links to the California Wildfires
InciWeb
http://www.inciweb.org/state/5/6/d/0/
InciWeb Maps
http://www.inciweb.org/maps/0/
Joe Maller – very good site
http://www.joemaller.com/california_wildfires2003.shtml
Battling California Wildfires
http://www.calfires.com/
Friday, October 19, 2007
7th honors POW
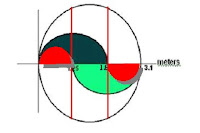
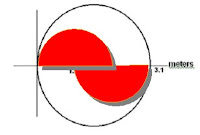
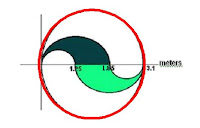
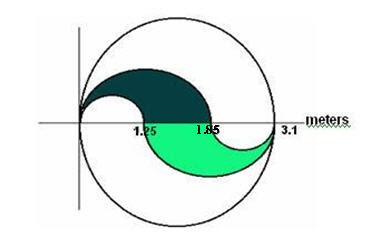
You then solve for the area of each of the three circles. If you do a bit of subtraction you can find out how much shaded, then white or ‘non-shaded’, and total fabric you needed for this logo.
Happy Friday! Just to let you know I am seeing a vast improvement in the caliber of your writing and your explainations. Please continue to write as if you are explaining the process to someone who does not understand how to proceed with the problem at all.
Here is your problem:
Jocie was decorating her notebook with her High School’s cheer logo. The School logo is shown below. The logo includes two different fabric types. The shaded and un-shaded pieces are made of different materials.
Questions to address:
1 - How much material does she need for the shaded area?
2 - How much material does she need for just the un-shaded area?
3 - Show the steps to your solution; make sure to explain every step as you write it.
(My bad I wrote meters it should be centimeters.)
Ms. L.
Friday, October 12, 2007
7th Grade Friday Blogger Work
Today I have provided a list of links for you to explore. I would like you to visit all of the sites listed. Complete the activities and then post a review of each of the sites.
Explain:
Did you liked the site and why?
Who would benefit from the site and why?
What was good about the site and what might the author of the page do to improve the
mathematics on the site.
Make sure to support your argument with examples from the sites.
Be sure to use complete sentences...
Sites:
Play each of the games at:
http://www.bbc.co.uk/education/mathsfile/gameswheel.html
(Just a tip in the past students have been intrigued with Builder Bob.)
http://www.bbc.co.uk/schools/ks3bitesize/maths/
http://www.visualfractions.com/
http://www.shodor.org/interactivate/activities/numbercruncher/
http://www.dositey.com/addsub/Mystery11.htm
http://www.funbrain.com/cgi-bin/gn2.cgi?A1=s&A2=10&A3=0&A14=1&A15=1
http://www.learningwave.com/abmath/hotel/index3a.html
Ms. Leckman
Friday, October 05, 2007
To Kill a Mockingbird

Please begin to investigate and address these issues. Be sure you are responsible, reflective, and respectful in your responses. These are to be answered using the 6+1 writing traits. I will be posting a rubric soon. Be thorough and comprehensive in your explanations. Use graphs or tables to support your findings. Be sure you are citing your data sources and supporting your explanation or rational with the statistics and mathematics behind your response. You should assume your reader has no knowledge in these topics. The reader should have enough information to understand and agree or disagree with your viewpoint and your mathematics.
Make sure you explicitly address how the features you choose become apparent in the book, To Kill a Mockingbird. How do you see your factors illustrated in the story or how does Harper Lee allow you to feel these factors in, To Kill a Mockingbird? How do these factors impact the characters and their actions in the story?
What were the population ratios of “Whites to Blacks?” in the early 1930’s?
What was the lifestyle of the Southern populations in the early 1930’s?
How much money did each socio-economic group make? For example: Upper, Middle, Lower socio-economic classes?
What was the average cost of living during this time? What did these kind of lifestyles look like? How are they the same or different than today?
What is the ratio of court cases of the defendant’s racial background? (Today compared to the 1930’s)
What were the ratios of Black, Latino or other “minority” attorneys in the 1930’s?
How would that impact the justice system (now and then if different?)
What was the ratio of “professionals” or “educated” “minorities” in the 1930’s?
What impact would these factors have on each classes place in society?
I look forward to your findings! :-) <(^^<) (>'-')>
Ms. L.
Friday, September 28, 2007
Reflection September 28th
Feeling like you are working too hard? Your probably not alone. Today we will not be doing a Problem of the Week, instead we will try to help each other. Here are your tasks for today. Do not copy and paste this writing into your reply!!!!
1. Look through your book and identify a couple areas you need help in for the assessment next week. (For 8th Grade: remember that the assessments are cumulative so that means there may be problems you would want help with from chapter one as well as chapter two.) You will need to post three questions or requests for help. (I can't think of one of you that should not be able to find three things you need help with... so don't go there. :-) ) You will want to find a problem in the book that illustrates the type of help you need.
2. You will go to the "I get by with a little help from my friends" blog and post your responses under the correct book and chapter/investigations. Post an example problem in your reply and explain what you need help understanding.
3. Make sure you post your reply under the correct chapter and book.
4. Next, find and respond to at least three post that need help. Be complete and give them as much help as you can.
5. Make sure to put your intials at the top of each of your posts so I can easily find them. (Thank you in advance.)
Good luck! Ms. L.
Monday, September 24, 2007
More about last weeks post
Last weeks POW was actually a version of a very old puzzle - The Tower of Hanoi or Towers of Hanoi. The Towers of Hanoi are a mathematical game or puzzle. It consists of three pegs, and a number of disks of different sizes which can slide onto any peg. The puzzle starts with the disks neatly stacked in order of size on one peg, the smallest at the top. The objective of the game is to move the entire stack to another peg. Easy, maybe but you have to follow the following rules: You may only move one disk at a time. You may only move the top disk from one of the pegs and sliding it onto another peg, it can be placed on another disk that may already be present on that peg. And finally, no disk may be placed on top of a smaller disk.
The puzzle was invented by the French mathematician Edouard Lucas in 1883. There is a legend that accompanies the game. It states there is a temple which contains a large room with three posts that contain 64 golden disks. According to the legend, when the last move of the puzzle is completed, the world will end. The priests of Brahma, acting out the ancient prophecy and have been moving these disks, in accordance with the rules of the puzzle. There are patterns which repeat the action over and over again, we call these iterative patterns. The Towers of Hanoi are a type of iterative pattern called a recursive pattern. A recursive pattern is a pattern that repeats itself but you have to have the results of the previous action or term to determine the outcome of the output or term you are solving for. This type of patterning is very common in computer programming and The Tower of Hanoi is a problem often used to teach beginning programming.
If you would like to try the original puzzle click on the link below:
http://www.vtaide.com/png/lesol/games/tower/hanoi-2j.html
Ms. Leckman
Monday, September 17, 2007
POW for the Week of September 17th
Ms. Leckman
Games away:
http://www.hellam.net/maths2000/frogs.html
Tuesday, September 04, 2007
Sept 4th POW
You may think about the problem.
You may try to solve the problem.
You may not post your responses until Friday while we are in the lab.
Before the start of the fall membership drive, Mrs. Roberts wants to know how many students are in the Mathematics Club.
She asks the president of the club, "What's your membership?"
The president replies, "twice our number plus half our number plus a quarter of our number plus you is one hundred."
"Great," says the Principal, "that is exactly one more than one eighth of our total student enrollment here at Madison Number One Middle School."
1. How many students are enrolled at Madison Number One Middle School?
2. How many students are in the Math Club?
3. Write an equation that will help you either find or justify your answer.
Be sure to use comprehensive explainations when you explain how you found each answer. Good Luck. Ms. L.
Friday, August 31, 2007
POW August 31st
:-) Good luck.
Ms. L.
P.S. Ma ke sure to put both you and your partnership intials in the box you submit your answers. I can't give you credit if I don't know who posted the response. :-)
Here is the POW for this week:
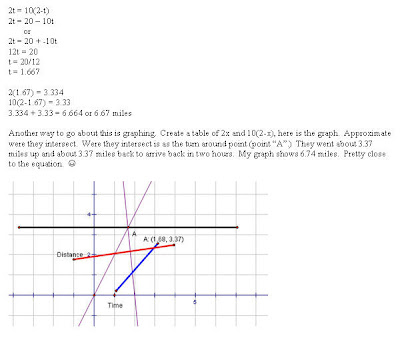
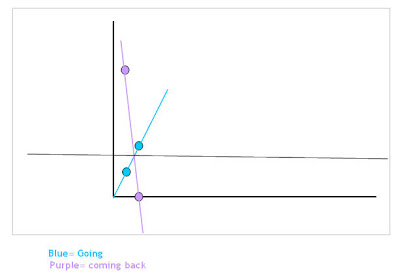
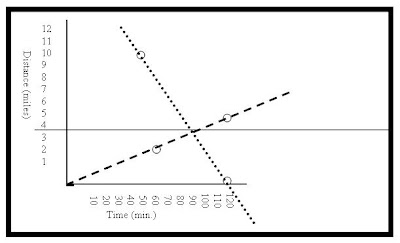
Doug and Anna plan to kayak on the river near their home. The river flows at a rate of 4 miles per hour. In still water they paddle their kayaks at a constant rate of 6 miles per hour. They start and end their trip at the same place on the river. They kayak for exactly two hours, first going upstream and then downstream. What is the total length, in miles, of their trip on the river? Express your answer as a decimal to the nearest hundredth.
You guys did a very nice job this week. Many of you were able to see that the distance there and back needed to be equivalent. The idea of writting them as two equations was a new idea to some of you. Here are two ways to look at the solution to this weeks problem.
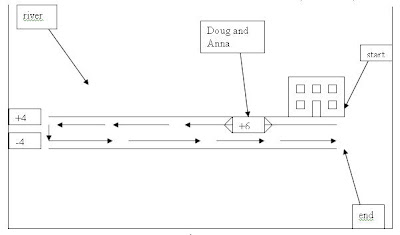
What's my line?