POW August 31st

You all did a nice job on last weeks problem. Here is a problem that you can use some of the "tools" we have been talking about in class. They may come in handy in solving this problem.
:-) Good luck.
Ms. L.

P.S. Ma ke sure to put both you and your partnership intials in the box you submit your answers. I can't give you credit if I don't know who posted the response. :-)

Here is the POW for this week:

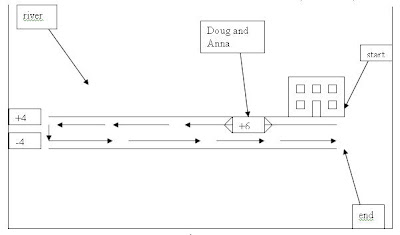
Doug and Anna plan to kayak on the river near their home. The river flows at a rate of 4 miles per hour. In still water they paddle their kayaks at a constant rate of 6 miles per hour. They start and end their trip at the same place on the river. They kayak for exactly two hours, first going upstream and then downstream. What is the total length, in miles, of their trip on the river? Express your answer as a decimal to the nearest hundredth.


You guys did a very nice job this week. Many of you were able to see that the distance there and back needed to be equivalent. The idea of writting them as two equations was a new idea to some of you. Here are two ways to look at the solution to this weeks problem.

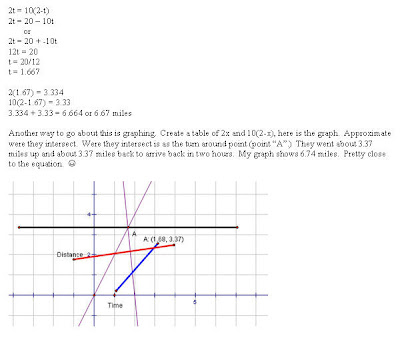
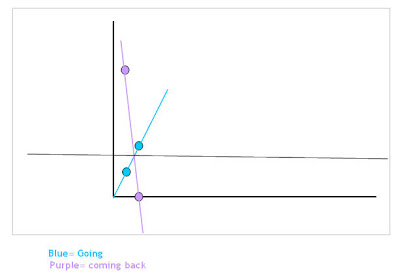
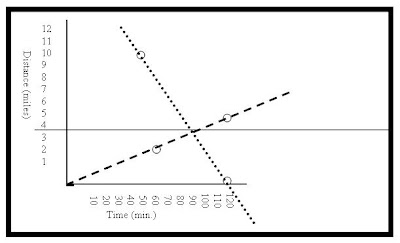
Here are some of your peers graphs and tables. :-)

POW Aug. 20th

O.k. so here is your first POW. I know all of you have received an e-mail like this one, but why do they work? Your task is to mathematically explain this quandary. Be as specific and concise as you can. (Remember - save a copy of your work in Word just in case. :-) and use your first and last initial ONLY!!!!)

Ms. JL


Many of you sent in excellent solutions to this problem!!! You tackled it using logic, order of operation, and algebra these are all great ways to go about solving the problem!

Here is the way the author of the problem saw the answer.

Please go back and look at the ways your peers solved the problem. Feel free to post comments, questions, or commend your peers for the way they approached the problem.

If x is the number you think of, you start with x,
Then when you add 1, you get x + 1
When you double it, it turns into 2x + 2
When you take away 3, it turns into 2x -1
Adding the number you first thought of makes 3x -1
When you add 7 it turns into 3x + 6
When you divide by 3 it turns into 1x + 2
Then take away the number you first thought of (x) it leaves 2.

See you Monday,
Ms. Leckman